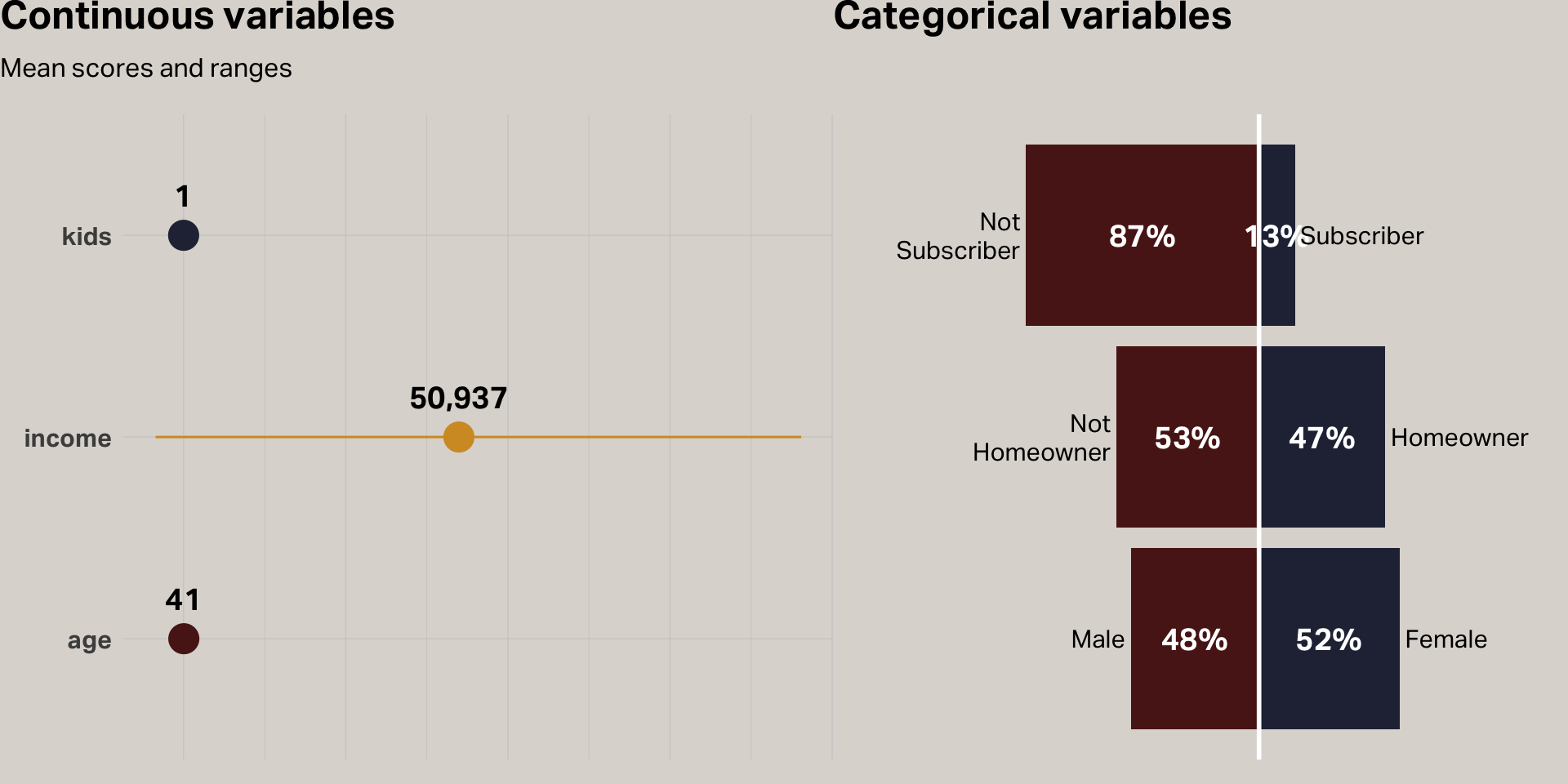
| Variable | Median | Mean | SD | Min | Max | NAs |
|---|---|---|---|---|---|---|
| age | 39 | 41.20 | 12.71 | 19 | 80 | 0 |
| female | 1 | 0.52 | 0.50 | 0 | 1 | 0 |
| income | 52,014 | 50,936.54 | 20,137.55 | −5,183 | 114,278 | 0 |
| kids | 1 | 1.27 | 1.41 | 0 | 7 | 0 |
| own_home | 0 | 0.47 | 0.50 | 0 | 1 | 0 |
| subscribe | 0 | 0.13 | 0.34 | 0 | 1 | 0 |
Clustering Customer Data
Overview
Using unsupervised learning techniques to divide customers into meaningful groups.
Presented by:
Larry Vincent,
Professor of the Practice
Marketing
Larry Vincent,
Professor of the Practice
Marketing
Presented to:
MKT 512
October 28, 2025
MKT 512
October 28, 2025
Why clustering?
- Group customers into meaningful segments based on shared needs, behaviors, attitudes, or preferences.
- Create targeted marketing strategies (MASDA)–measurable, accessible, substantial, differentiable, and actionable.
- With clearly defined segments, marketing resources can be allocated more effectively.
- Segmentation clusters also allow marketers to tailor products, messaging, pricing, and promotions to specific customer preferences.
- Uncovers hidden patterns and relationships in customer data, informing product development, positioning, and competitive strategy.
Example: Pet Food
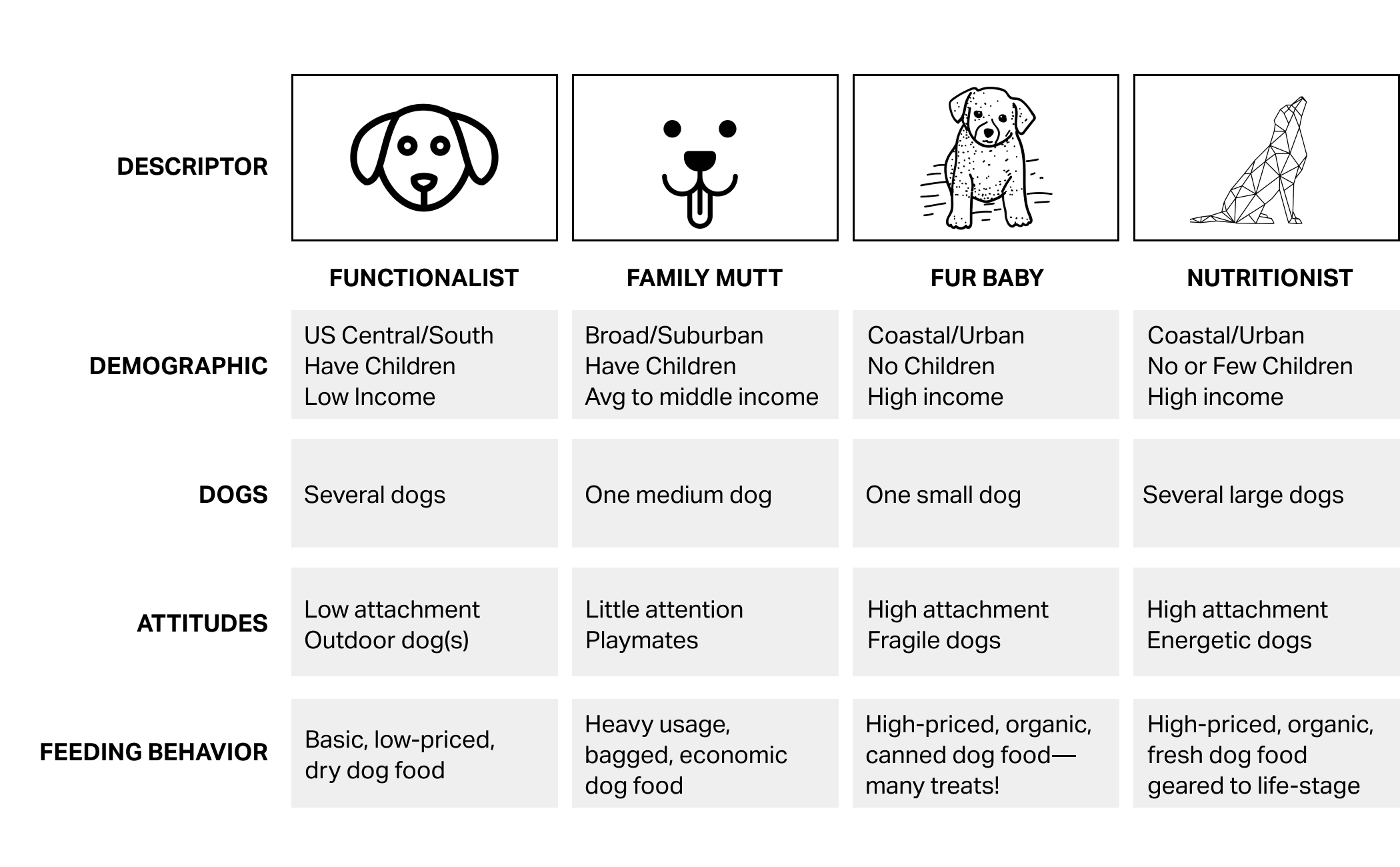
Case example
Le Abode
- Le Abode is a blog and e-commerce brand known for vintage-inspired, limited-edition home furnishings that rapidly sell out.
- Endorsed by influential figures; strong growth from consumers investing more in home environments.
- To better understand customer needs, preferences, and potential product directions, Le Abode’s team is exploring customer segmentation using demographic and behavioral data.
- Dataset includes demographics such as age, income, home ownership, household size (kids), gender, and subscription to Le Abode’s priority reservation program.
Data inspection
Analysis questions
- Any consistent patterns? If so, what are they?
- What are differences in segments in each model?
- How actionable are the segmentation suggestions for each model? Could you target customers with these suggestions? Would they be useful in developing or improving marketing mix?
Unsupervised learning
A statistical approach in which algorithms identify patterns or structures in data without pre-labeled outcomes or dependent variables. In the context of segmentation, it is used to discover natural groupings within the data—such as clusters of customers—based solely on their similarities and differences across selected variables.
Considerations
- Choosing the best method given data types (numeric, categorical, mixed), dataset size, interpretability, and desired outcome.
- Determining number of clusters–these methods require pre-selection.
- Do you need to normalize or pre-process variables appropriately to avoid skewed results driven by scale differences?
- Interpretation of results–Clusters or factors must be examined qualitatively because algorithmic results alone are usually insufficient for actionable marketing decisions.
- Test stability of segments or components by varying parameters or using validation subsets to ensure robustness (it is often an iterative process).
K-Means
K-means clustering
- K-means clustering partitions data into k distinct clusters by assigning each data point to the cluster with the nearest centroid (mean).
- Best suited when working with large datasets, numeric variables, and when the number of clusters (k) can be specified in advance.
- Differentiated from other methods by its computational efficiency and simplicity, although it’s sensitive to outliers and initial centroid placement.
- Practical considerations: Requires standardizing variables; multiple runs with different initializations recommended to ensure stability and consistency.
Different data types
and scales
Pre-Processing with PCA
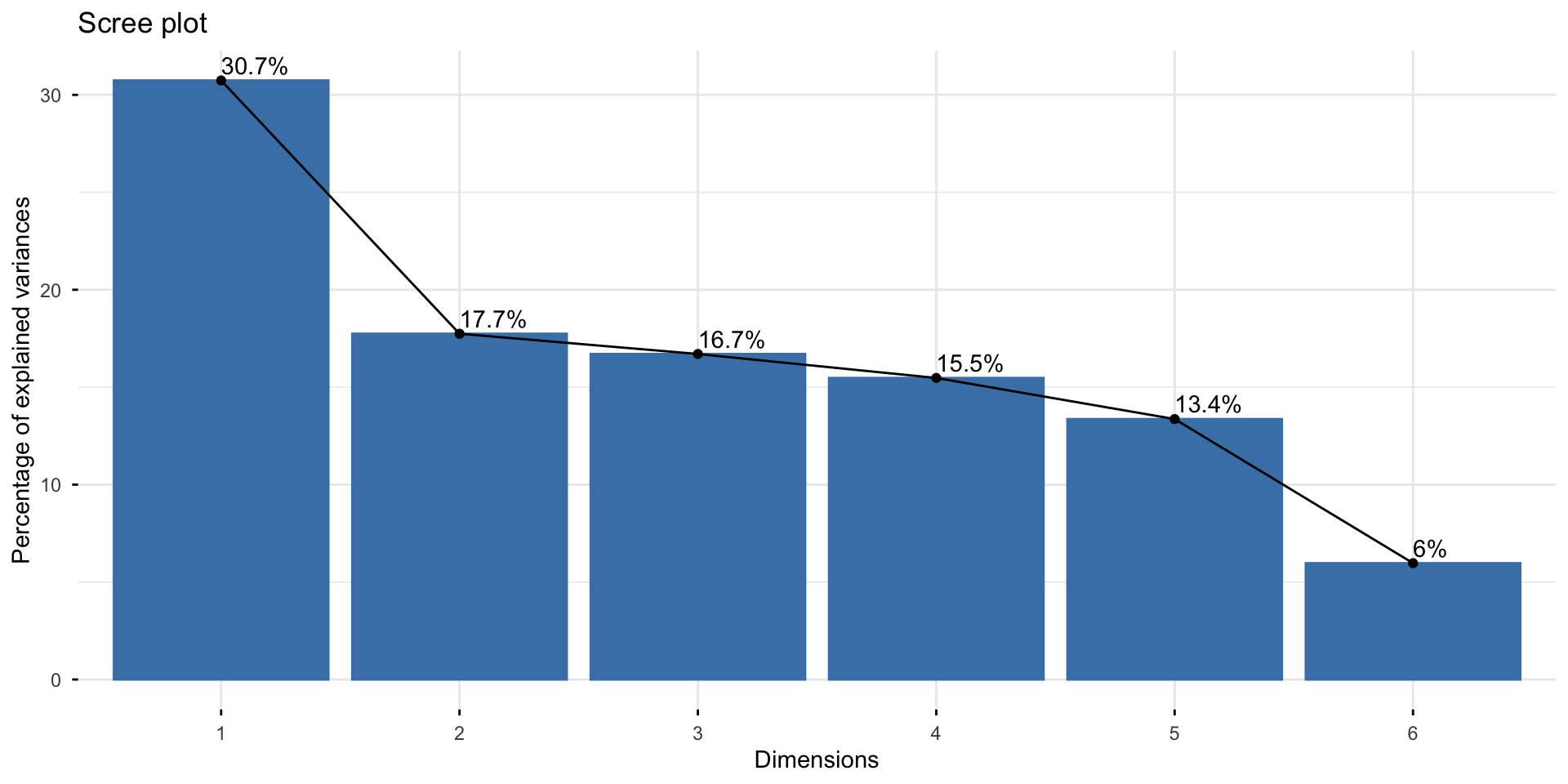
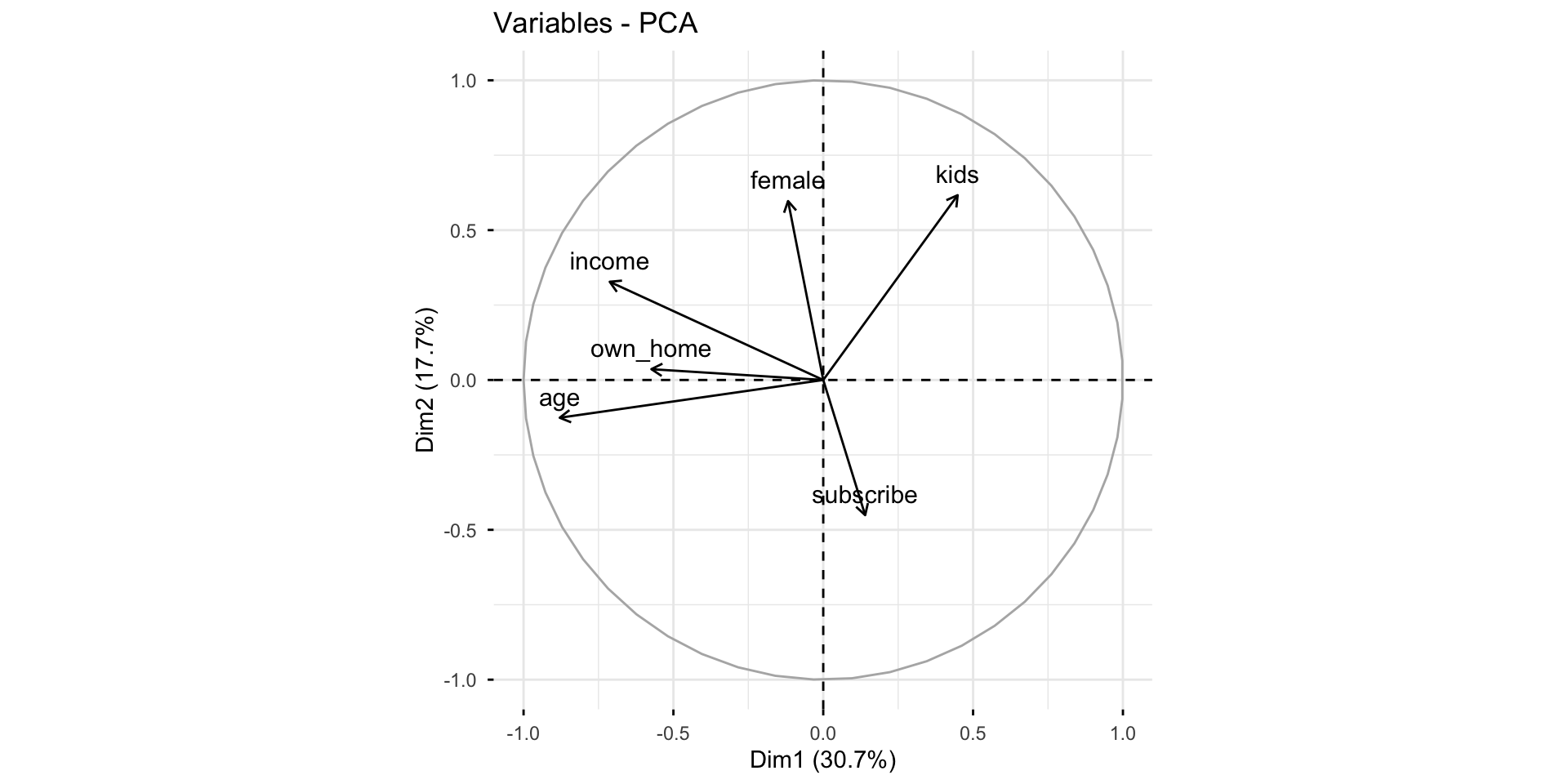
PCA
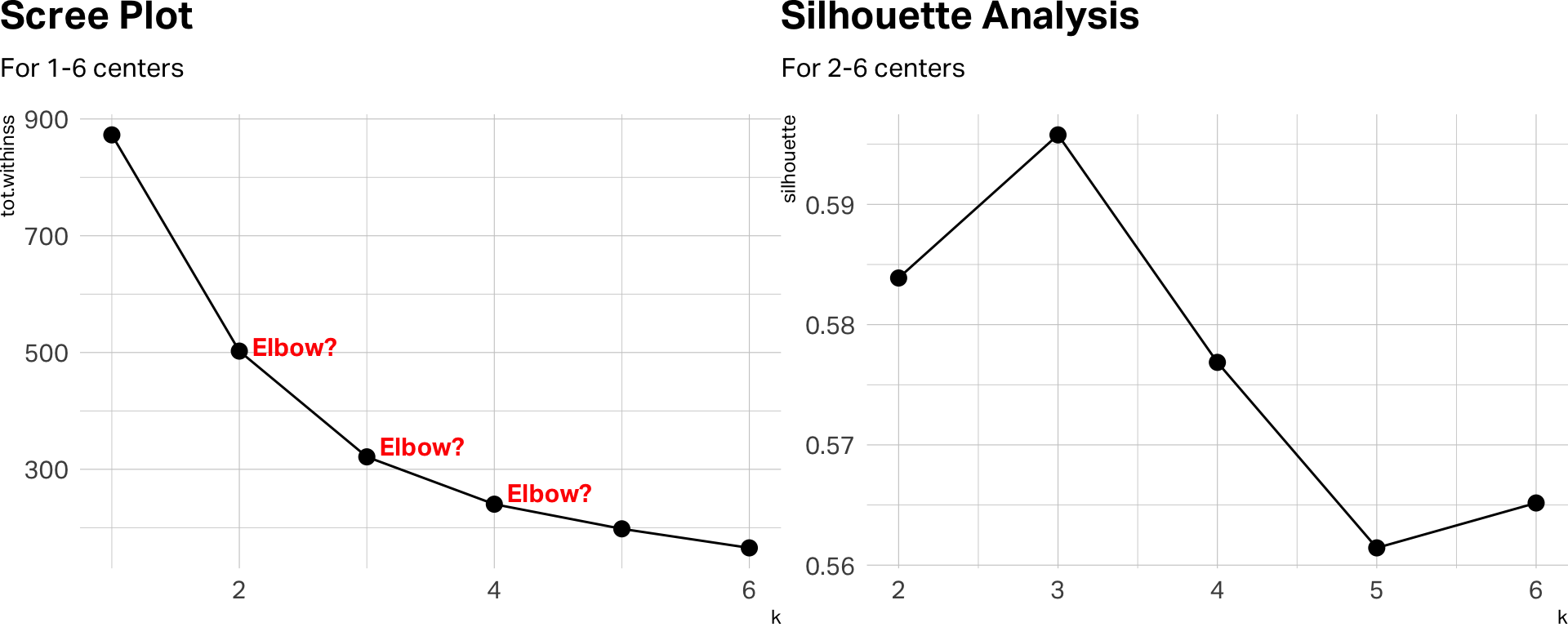
How many centers?
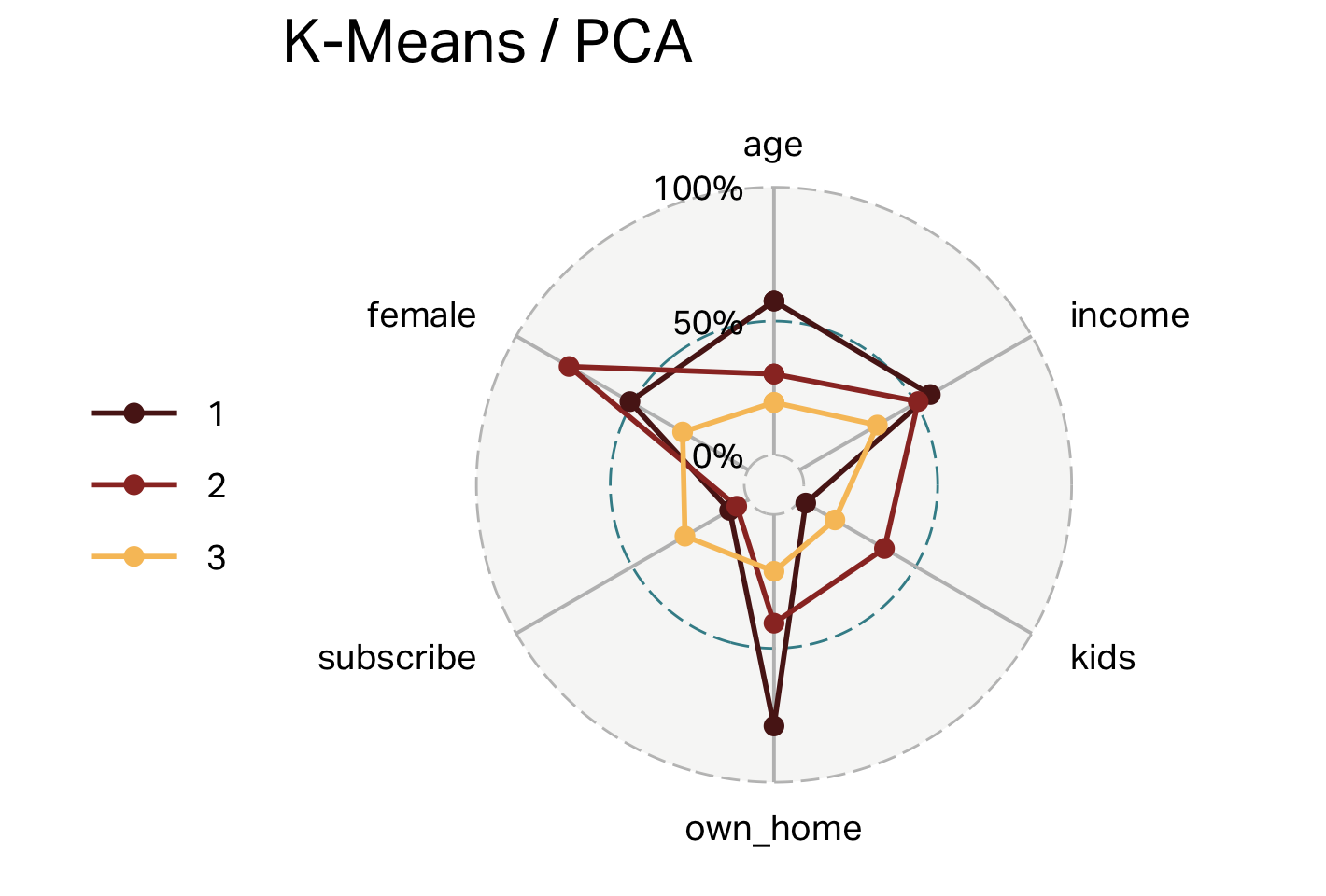
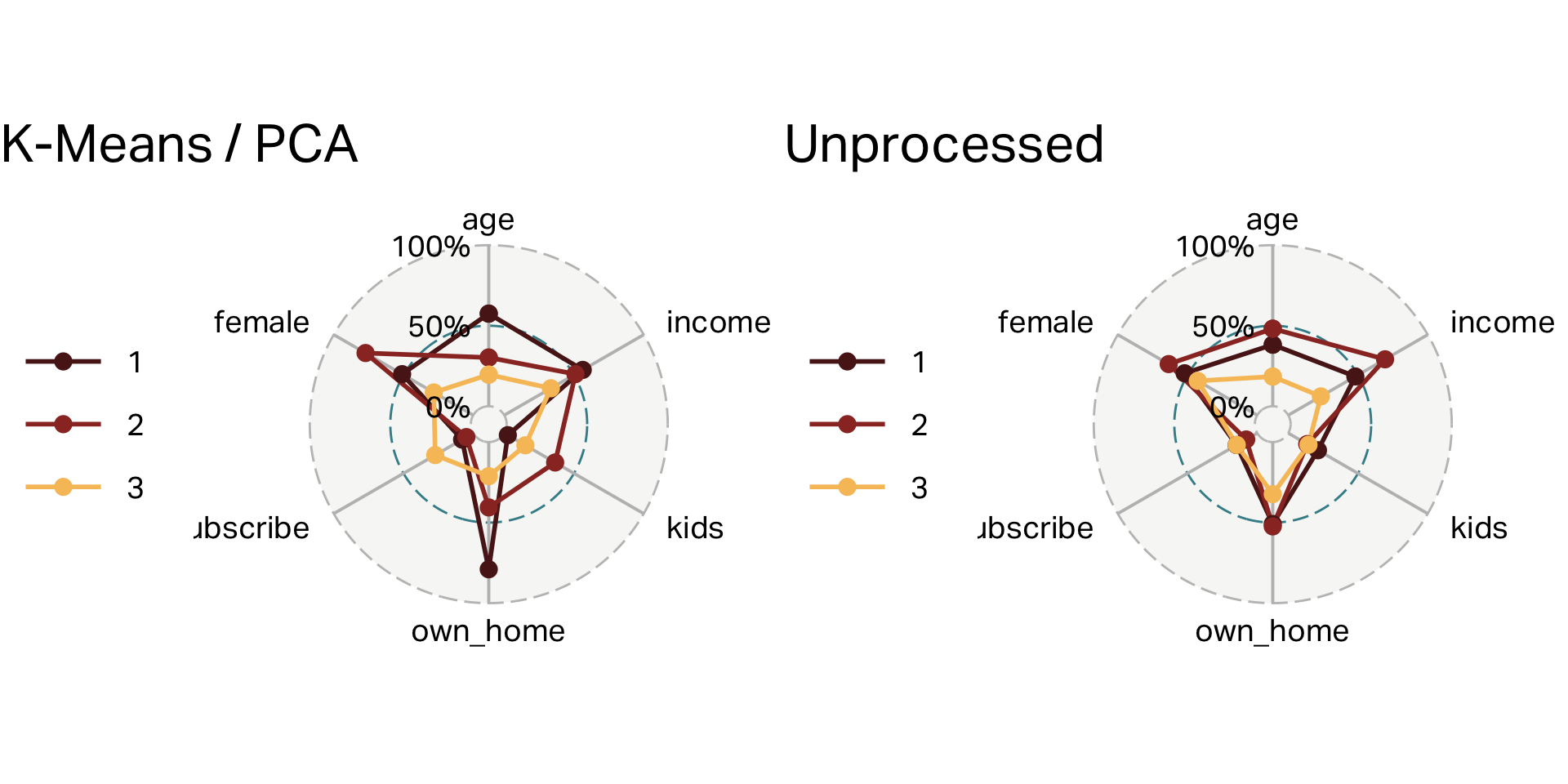
Three clusters (K-means)
| cluster | n | age | income | kids | own_home | subscribe | female |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 55 | 60,107 | 0 | 79% | 8% | 51% |
| 2 | 101 | 38 | 56,016 | 3 | 41% | 5% | 77% |
| 3 | 99 | 28 | 28,270 | 1 | 21% | 27% | 28% |
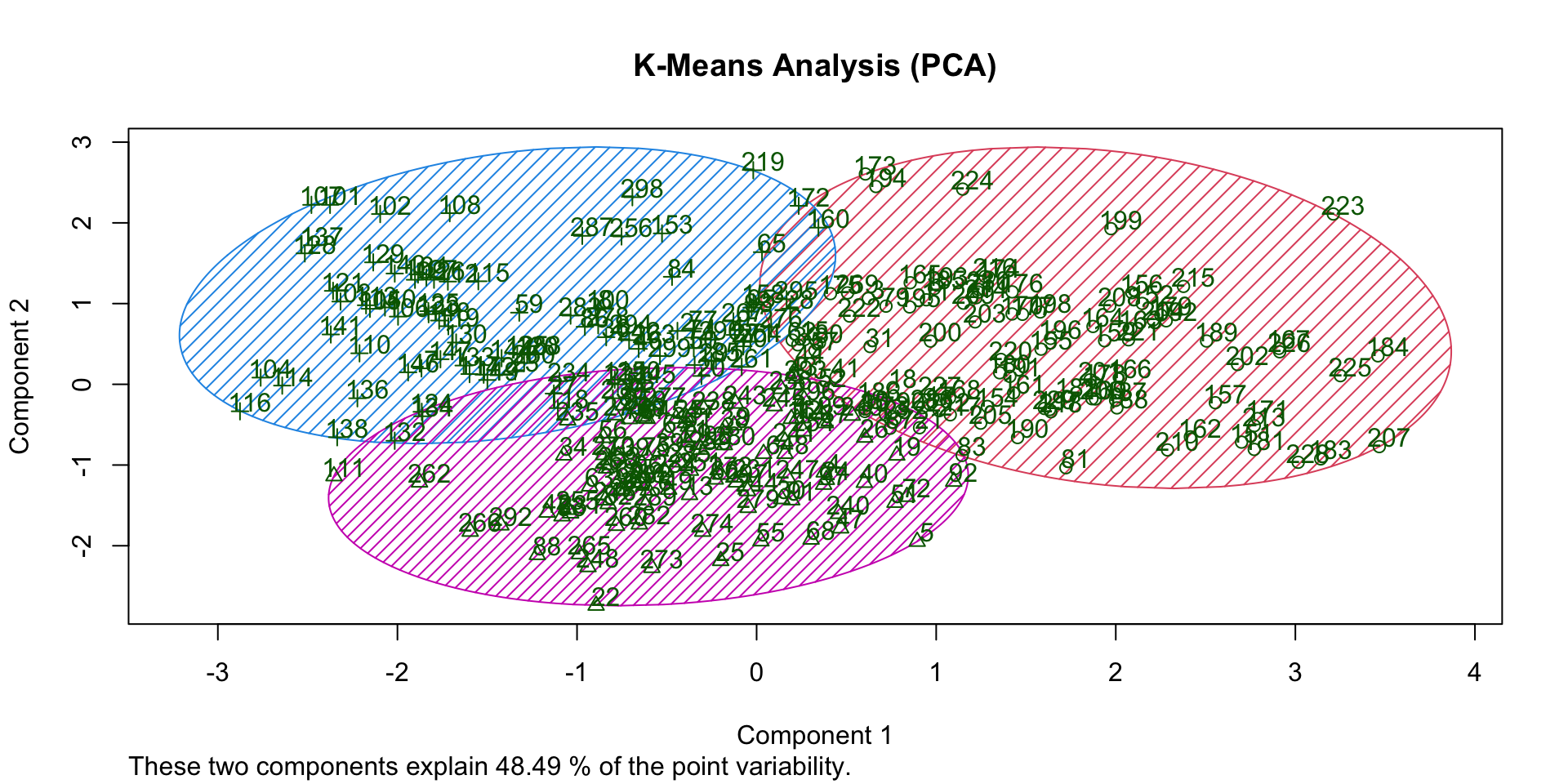
Overlap (K-Means)
FAMD
- Factor Analysis of Mixed Data (FAMD) is a dimension-reduction technique specifically designed for datasets containing both continuous (numeric) and discrete (categorical) variables.
- Best suited as an alternative to PCA when dealing with mixed variable types, allowing simultaneous analysis without converting or omitting variables.
- Differentiated from PCA by handling categorical variables directly, capturing associations between numeric and categorical variables effectively.
- Practical considerations: Results can be visualized similarly to PCA; scaling or standardizing numeric variables remains important; optimal when interpreting relationships across diverse data types.
FAMD
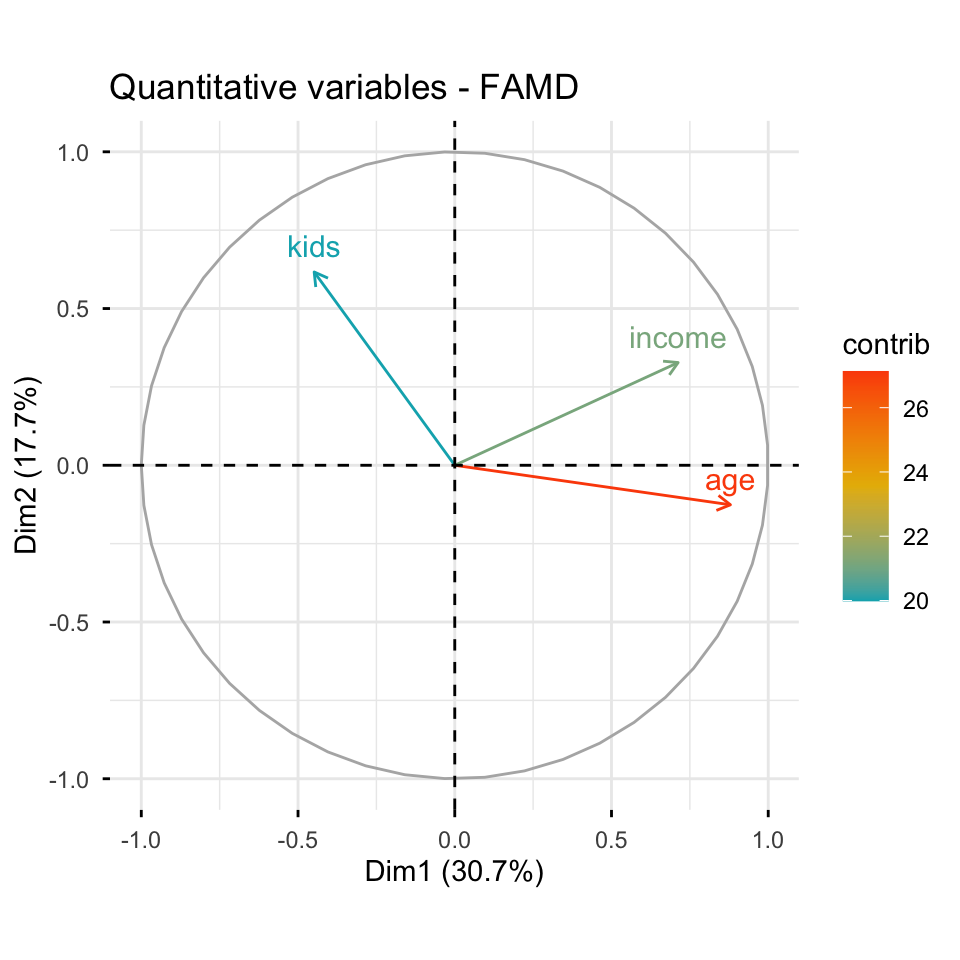
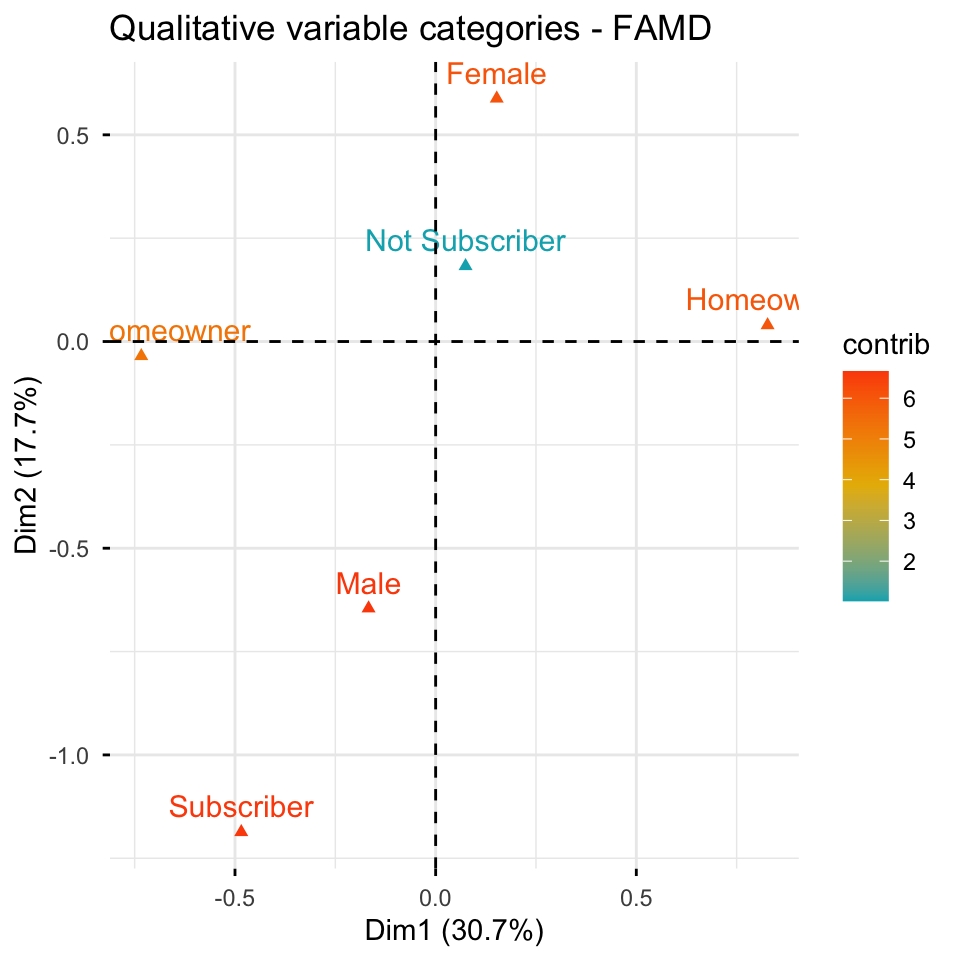
Three clusters (FAMD)
| cluster | n | age | income | kids | own_home | subscribe | female |
|---|---|---|---|---|---|---|---|
| 1 | 99 | 28 | 28,270 | 1 | 21% | 27% | 28% |
| 2 | 101 | 38 | 56,016 | 3 | 41% | 5% | 77% |
| 3 | 100 | 55 | 60,107 | 0 | 79% | 8% | 51% |
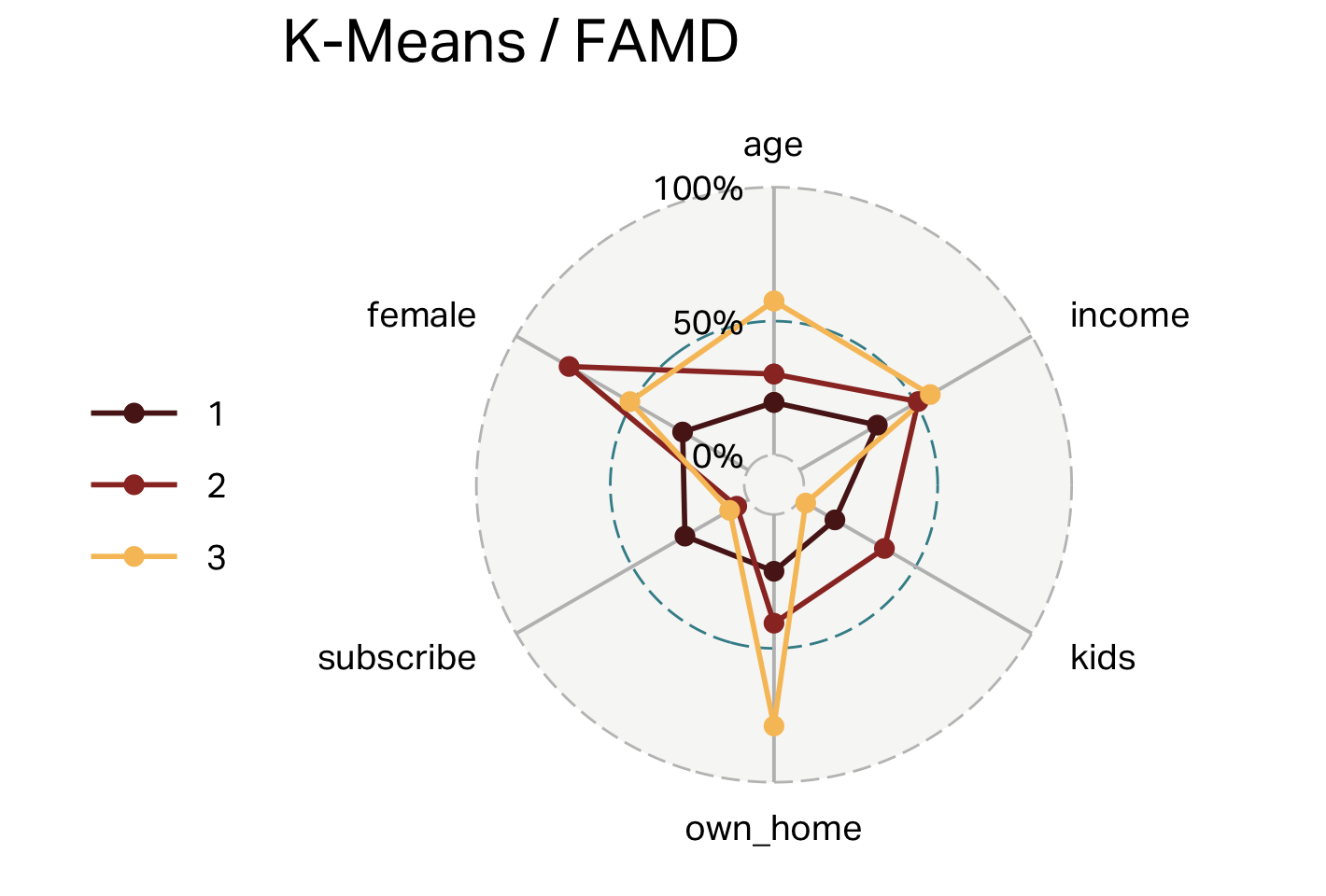
Overlap (FAMD)

Comparison
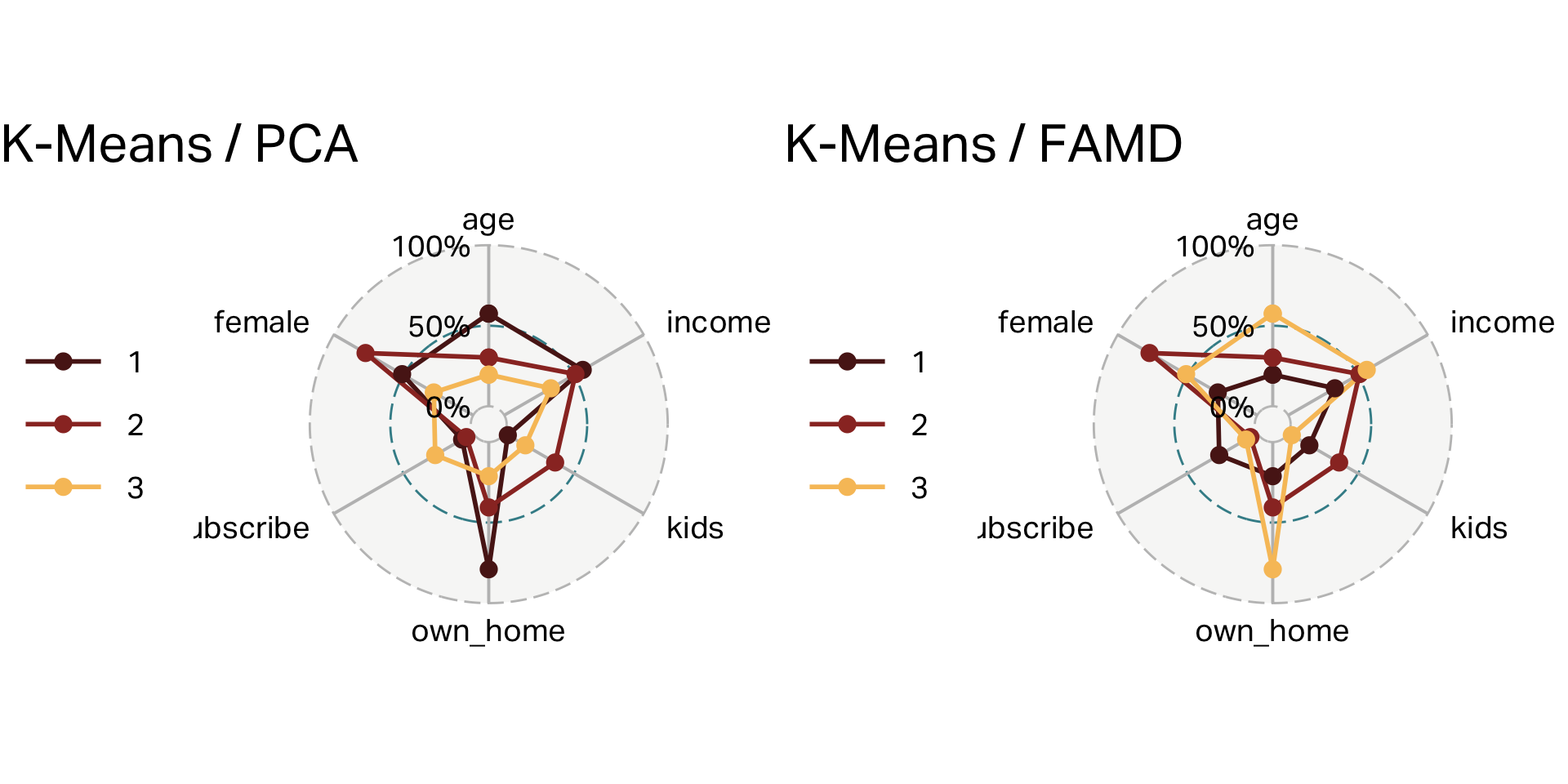
What if we didn’t process at all?
K-Means with no pre-processing
| cluster | n | age | income | kids | own_home | subscribe | female |
|---|---|---|---|---|---|---|---|
| 1 | 169 | 41 | 52,298 | 1 | 51% | 15% | 52% |
| 2 | 63 | 48 | 73,241 | 0 | 52% | 8% | 63% |
| 3 | 68 | 25 | 22,979 | 1 | 32% | 15% | 43% |
K-Means with no pre-processing
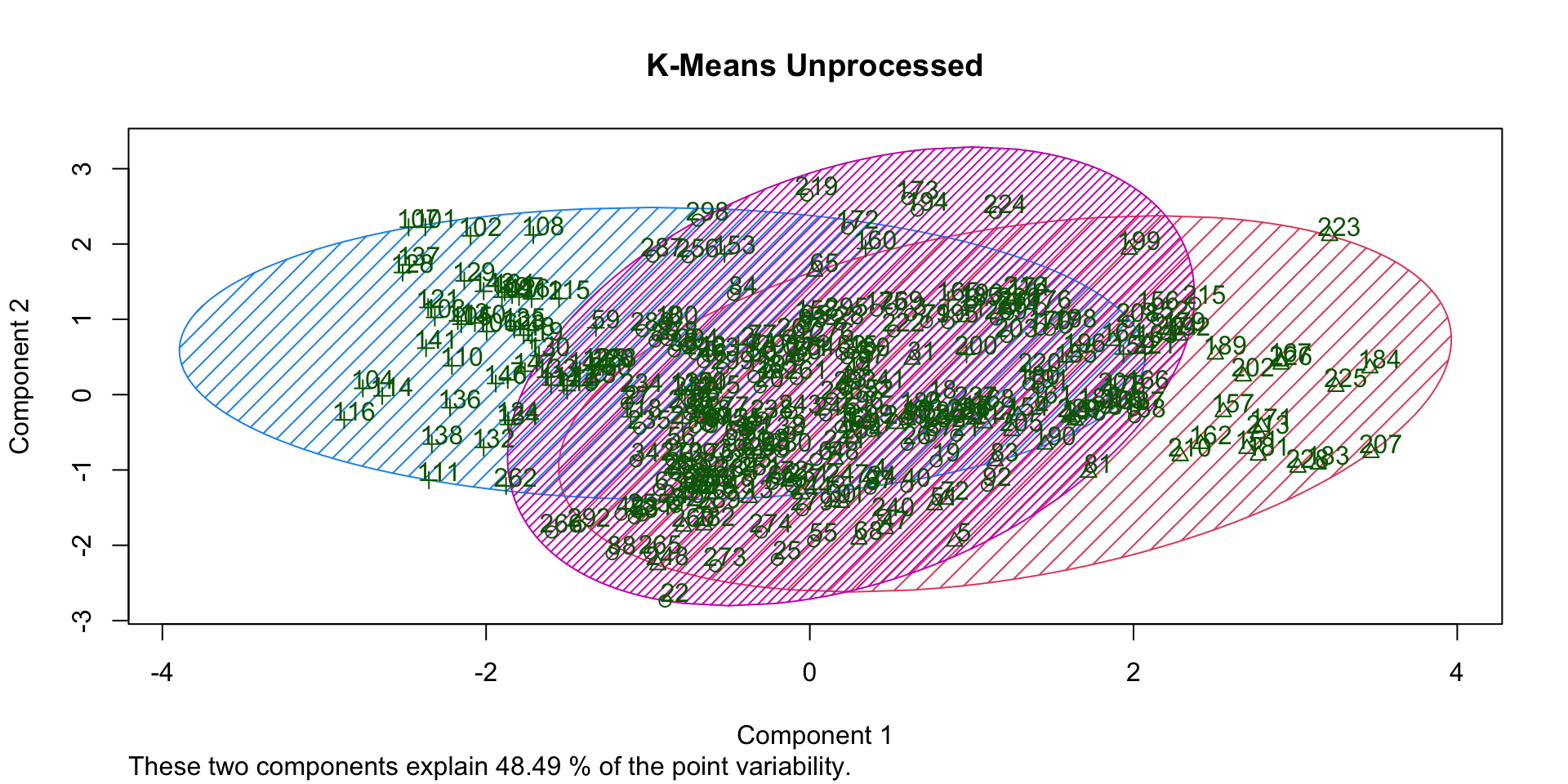
Overlap (no processing)
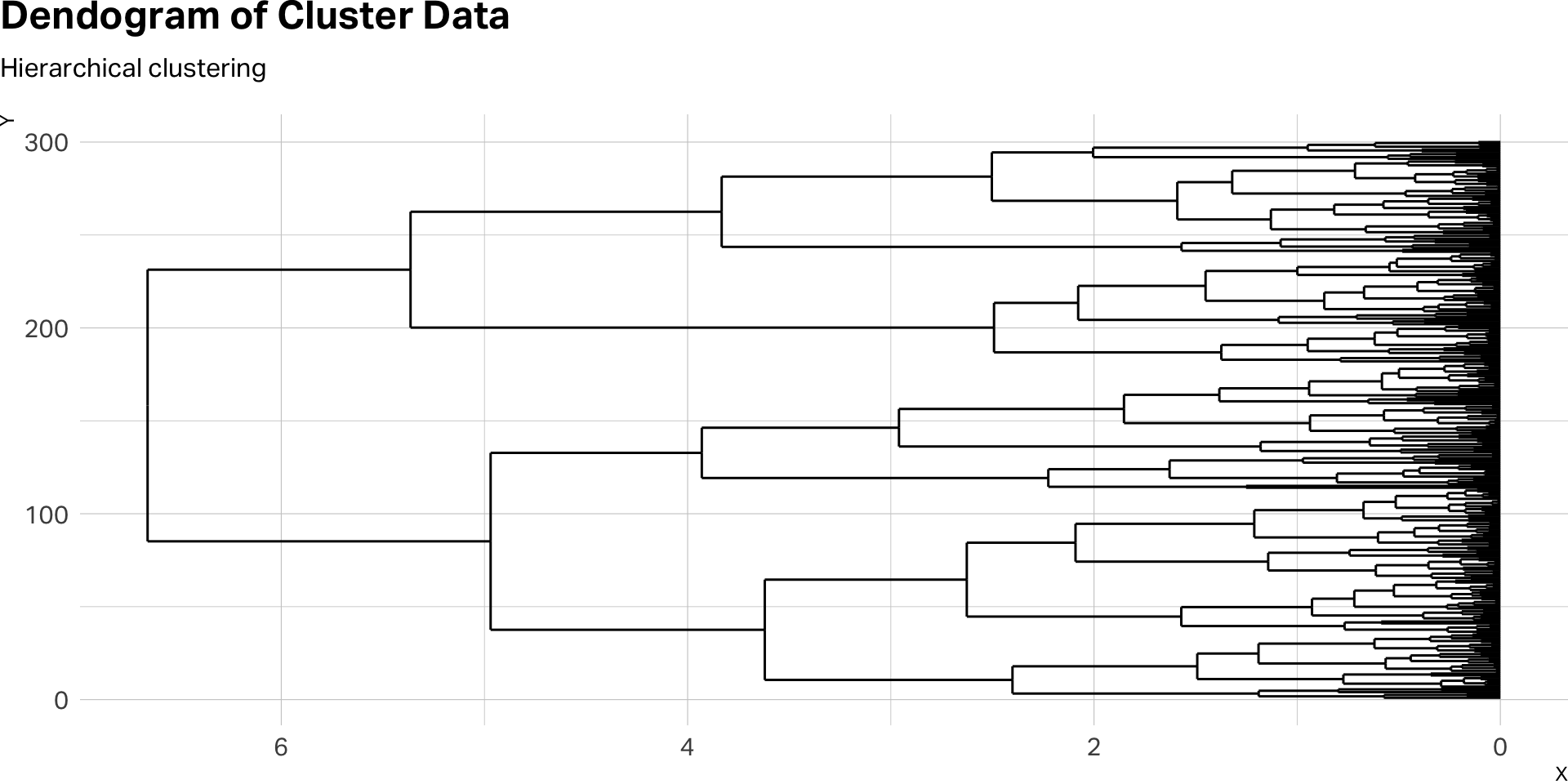
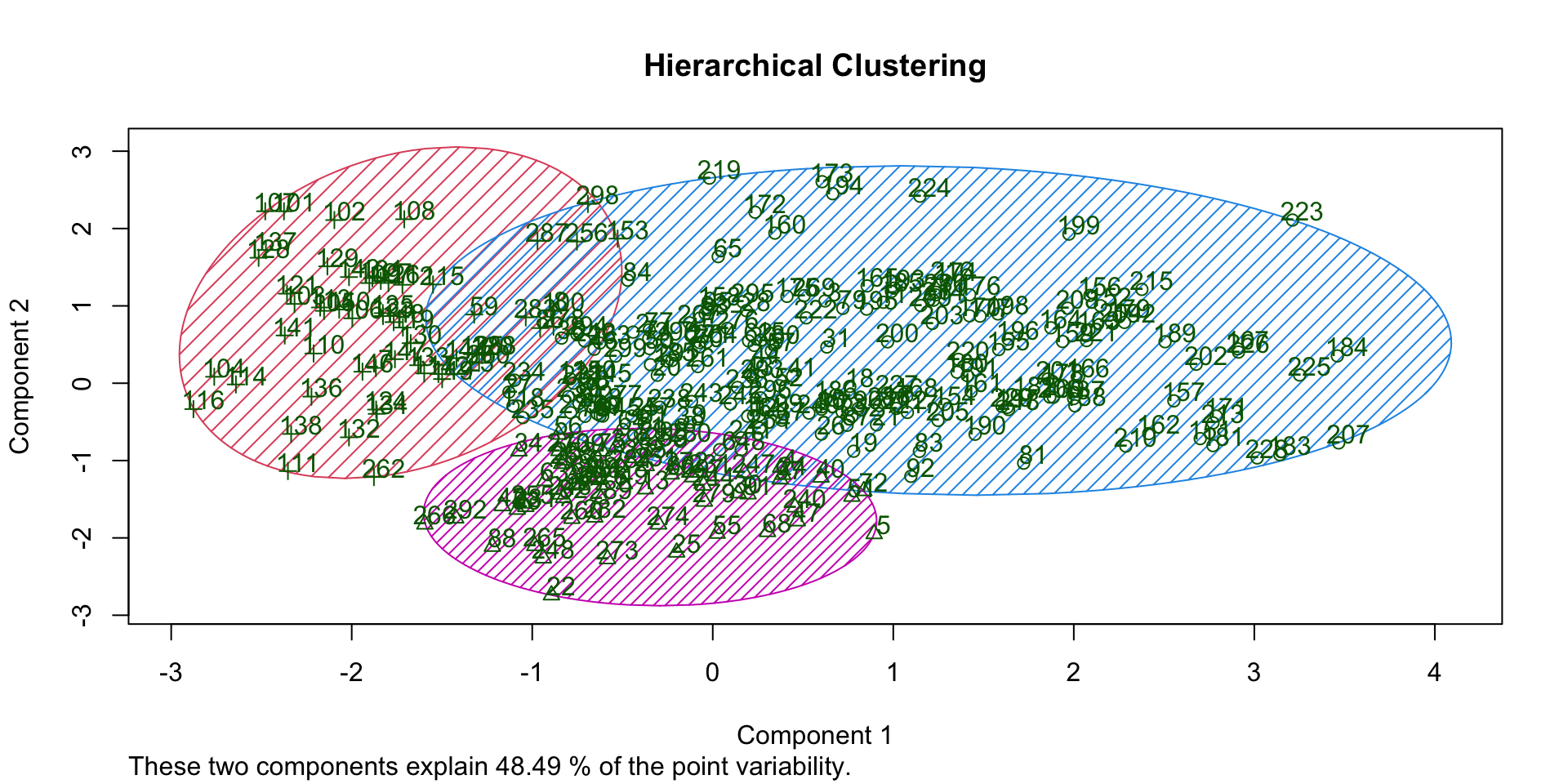
Hierarchical clustering
Hierarchical clustering
- Hierarchical clustering is a method that builds nested clusters by iteratively merging or splitting data points based on similarity, resulting in a dendrogram that visualizes cluster relationships.
- Best suited when the number of clusters is unknown upfront or when visualizing cluster structures at multiple levels of granularity is valuable.
- Differentiated from other methods (like k-means or PAM) by its hierarchical, tree-like structure, allowing flexible selection of the number of clusters after analysis.
- Practical considerations: Computationally demanding for very large datasets; sensitive to chosen distance metrics and linkage criteria (e.g., single, complete, average linkage).
Dendograms
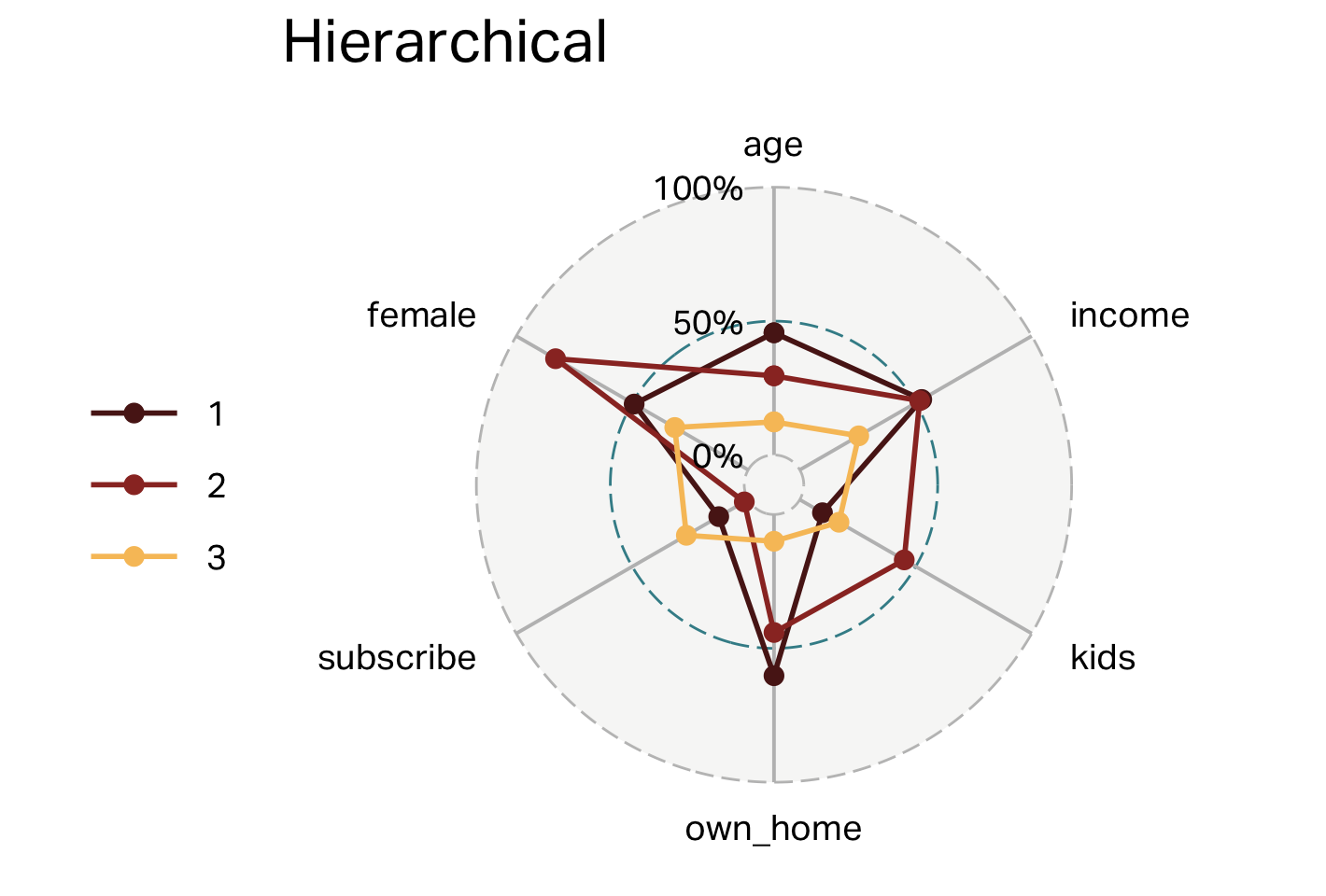
Clusters (HC)
| segment | n | age | income | kids | own_home | subscribe | female |
|---|---|---|---|---|---|---|---|
| 1 | 181 | 45 | 57,037 | 0 | 60% | 13% | 49% |
| 2 | 59 | 38 | 54,509 | 3 | 44% | 2% | 83% |
| 3 | 60 | 25 | 23,116 | 1 | 10% | 27% | 32% |
Overlap (HC)
PAM clustering
PAM
- Partitioning Around Medoids (PAM) is a clustering algorithm that groups data points around representative medoids—actual data points that serve as cluster centers.
- Best suited for situations with smaller datasets or when data contains outliers, as medoids are robust and less sensitive to extreme values.
- Differentiated from methods like k-means by using real data points as cluster centers (medoids), rather than computed averages (centroids), enhancing interpretability and stability.
- Practical considerations: Computationally intensive on large datasets; consider using faster variants (e.g., CLARA) for bigger samples.
Clusters (PAM)
| segment | n | age | income | kids | own_home | subscribe | female |
|---|---|---|---|---|---|---|---|
| 1 | 96 | 31 | 28,793 | 1 | 21% | 28% | 26% |
| 2 | 103 | 54 | 60,168 | 0 | 80% | 9% | 52% |
| 3 | 101 | 38 | 55,847 | 3 | 39% | 4% | 77% |
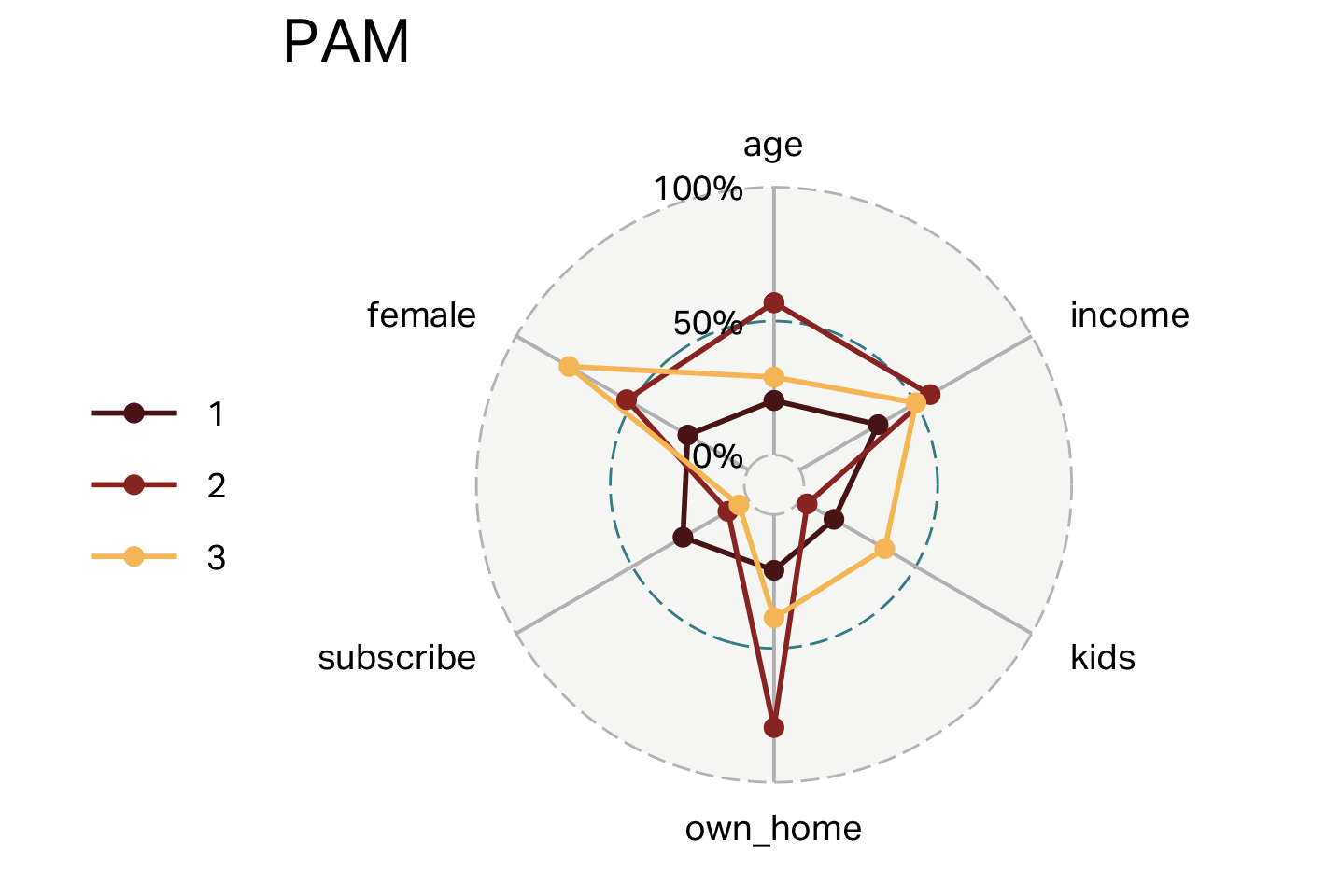
Overlap (PAM)

Latent Class Analysis
Latent Class Analysis
- Latent Class Analysis (LCA) identifies unobserved (“latent”) segments based on patterns in categorical or binary variables, using probabilistic modeling.
- Best suited for clustering respondents based on survey or categorical data, particularly when dealing with psychological, attitudinal, or preference measures.
- Differentiated from other methods by modeling underlying segment membership probabilistically, allowing respondents to belong partially (with probabilities) to multiple segments rather than just one.
- Practical considerations: Requires larger sample sizes for reliable segment solutions; selecting the number of segments typically involves comparing model-fit statistics (e.g., AIC, BIC).
Clusters (LCA)
| segment | n | age | income | kids | own_home | subscribe | female |
|---|---|---|---|---|---|---|---|
| 1 | 104 | 55 | 58,215 | 0 | 77% | 11% | 42% |
| 2 | 126 | 37 | 55,613 | 2 | 33% | 8% | 72% |
| 3 | 70 | 25 | 24,872 | 1 | 29% | 27% | 31% |
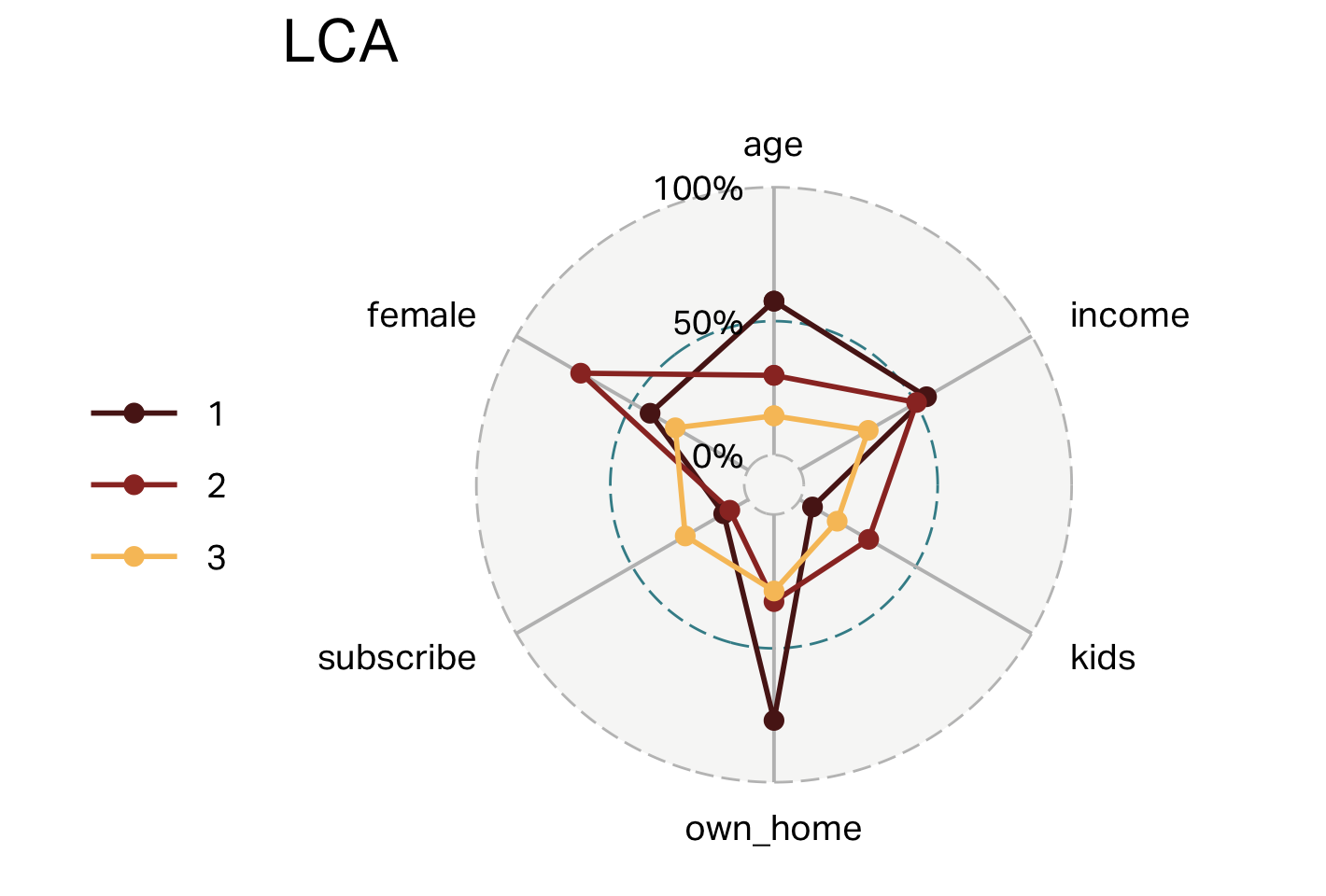
Overlap (LCA)

Your turn
![]()
- Select one clustering method
- Describe how it could be used to target customers
- Label the clusters with a meaningful descriptor
Clusters




