| Coffee Shop | ||
| Contribution Analysis | ||
| Item | Dollars | Percent |
|---|---|---|
| Revenue | $1,743 | 100% |
| COGS | $829 | 48% |
| Gross Margin | $914 | 52% |
| Service Costs | $472 | 27% |
| Transaction Fees | $45 | 3% |
| Contribution | $397 | 23% |
Determing the Value of a Customer
Overview
Understanding how customers create value for the firm and what customers value from the firm’s activities.
Larry Vincent,
Professor of the Practice, Marketing
MKT 512
September 2, 2025
Housekeeping
- Register a team or take matchmaking survey by midnight tonight
- Unassigned students will be sorted into teams by Thursday
- Don’t forget pre-semester poll; counts toward participation
- Please sign in on the seating chart that’s going around
- Experimenting with design; feedback welcome
- For this session, we will reference some Google Sheets. The link is available on Brightspace and the class Slack channel
Quick Review

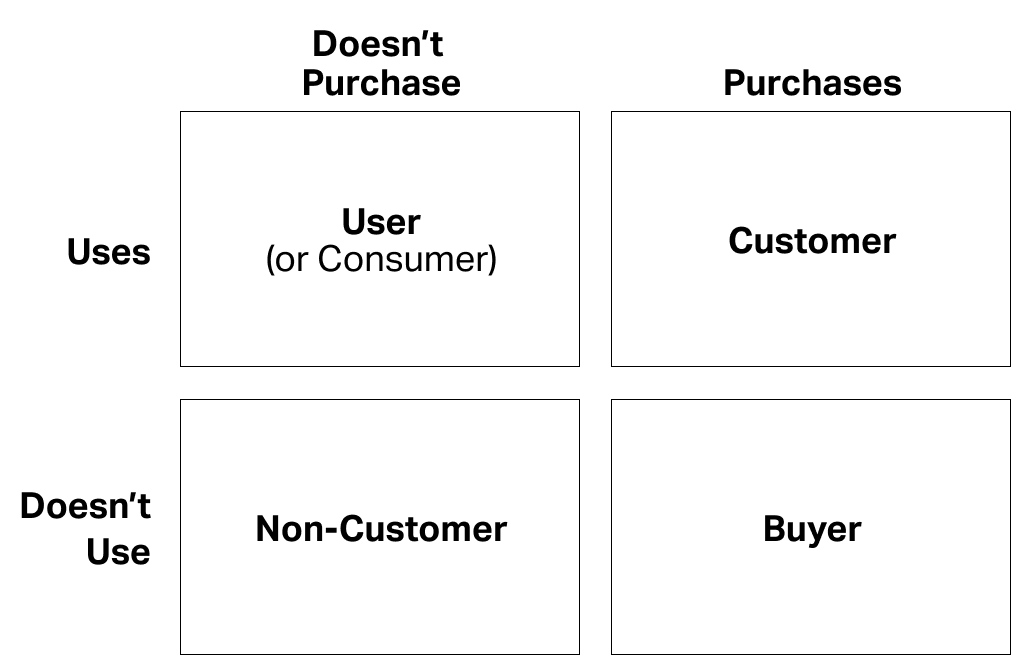
What’s the difference between a customer, a buyer, and a user?
Customers vs Others
Madmen Coffee
Recent Performance Analysis
| Coffee Shop | ||||
| Revenue Segmentation | ||||
| Segment | Revenue | COGS | Margin ($) | (%) |
|---|---|---|---|---|
| Beverages | 1,109 | 462 | 647 | 58% |
| Food | 634 | 368 | 267 | 42% |
Product Line

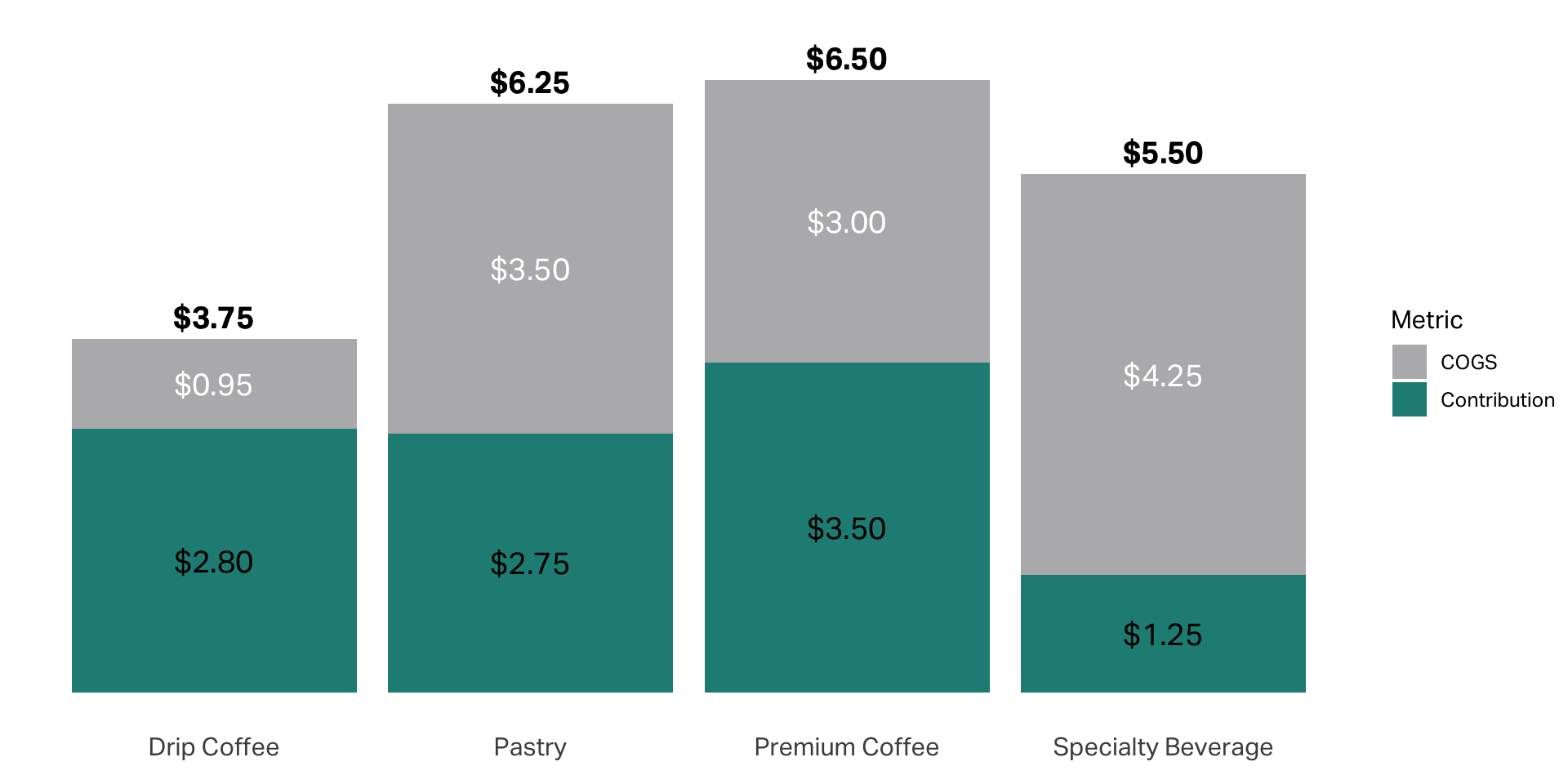
Premium Coffee
Price: $6.50
Cost: $3.00
Margin: 52%

Drip Coffee
Price: $3.75
Cost: $0.95
Margin: 74%

Pastry
Price: $6.25
Cost: $3.50
Margin: 42%

Specialty Beverage
Price: $5.50
Cost: $4.25
Margin: 17%
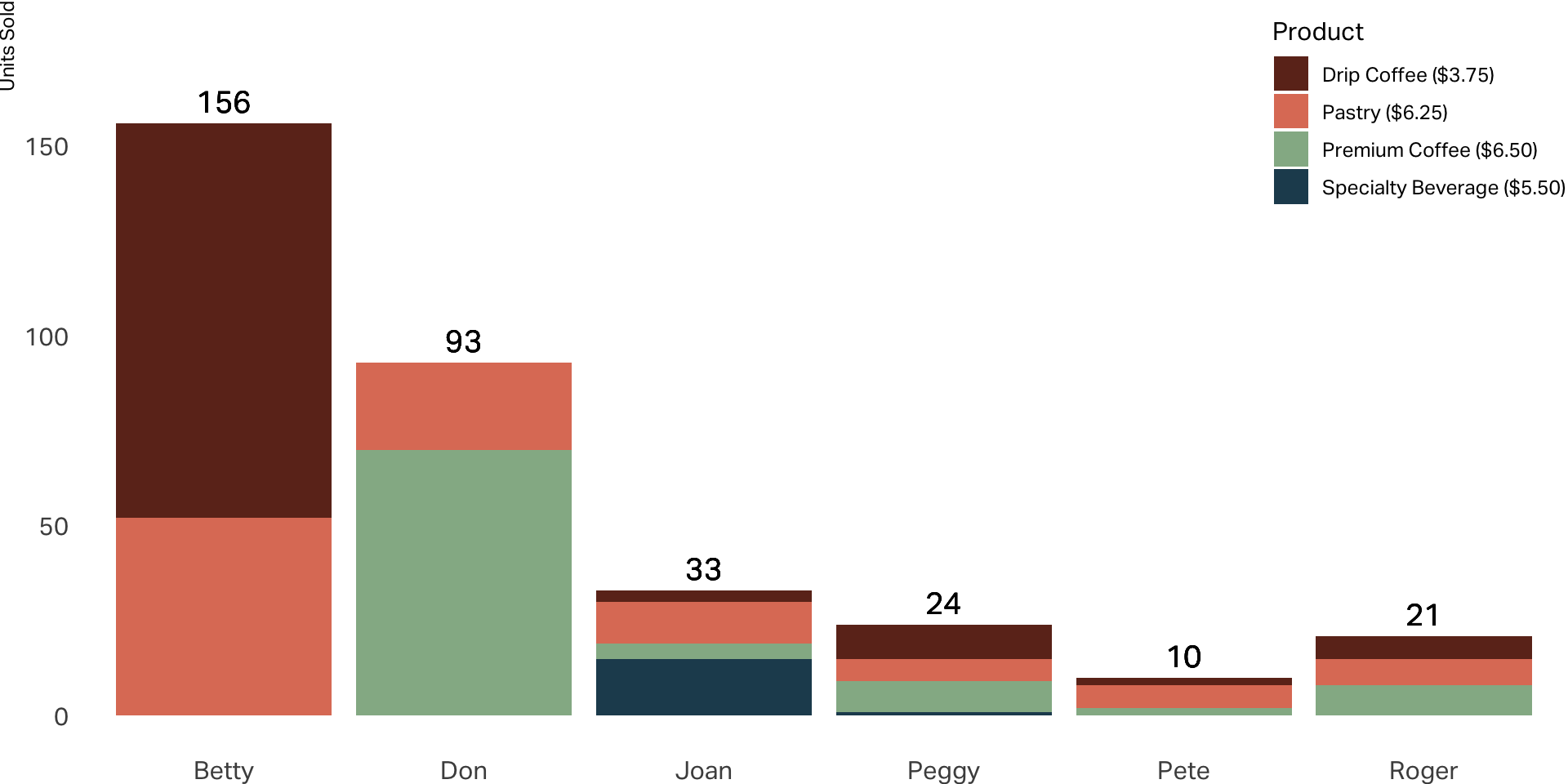
Product Performance
Customers

Betty
- Visits almost daily; Dines in
- Drip coffee and sometimes pastry
- Knows staff by name; gives them birthday cards; socializes

Don
- Local real estate agent
- Flat white–hot; will send back if there is too much foam or temp is off
- Often dines with guests; usually picks up the tab

Joan
- Visits 1-2x week
- Enjoys specialty/seasonal drinks
- Follows on social media; posts pics of drinks; on her phone constantly
Customers

Roger
- Referred by Don
- Visits occasionally, usually around mid-day; orders variety of items
- Business executive who lives in area

Peggy
- Referred by Joan
- Visits frequently and works on laptop and sometimes Zooms in store
- Good tipper; might be dating one of the baristas

Pete
- New customer; only a few visits so far
- Buys promotional items; uses discount codes
- Special requests and modifies orders
Average check
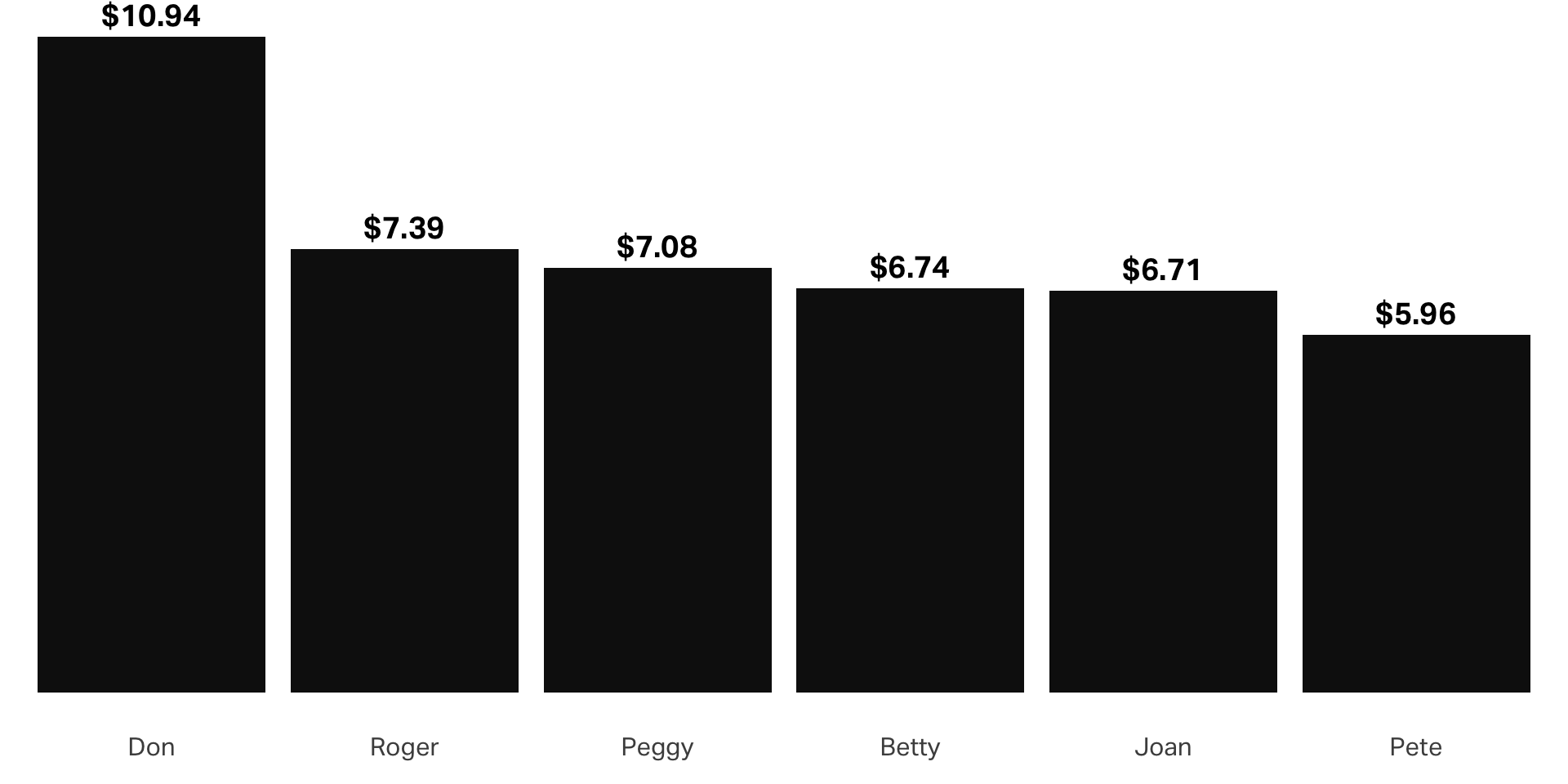
Unit Sales by Customer
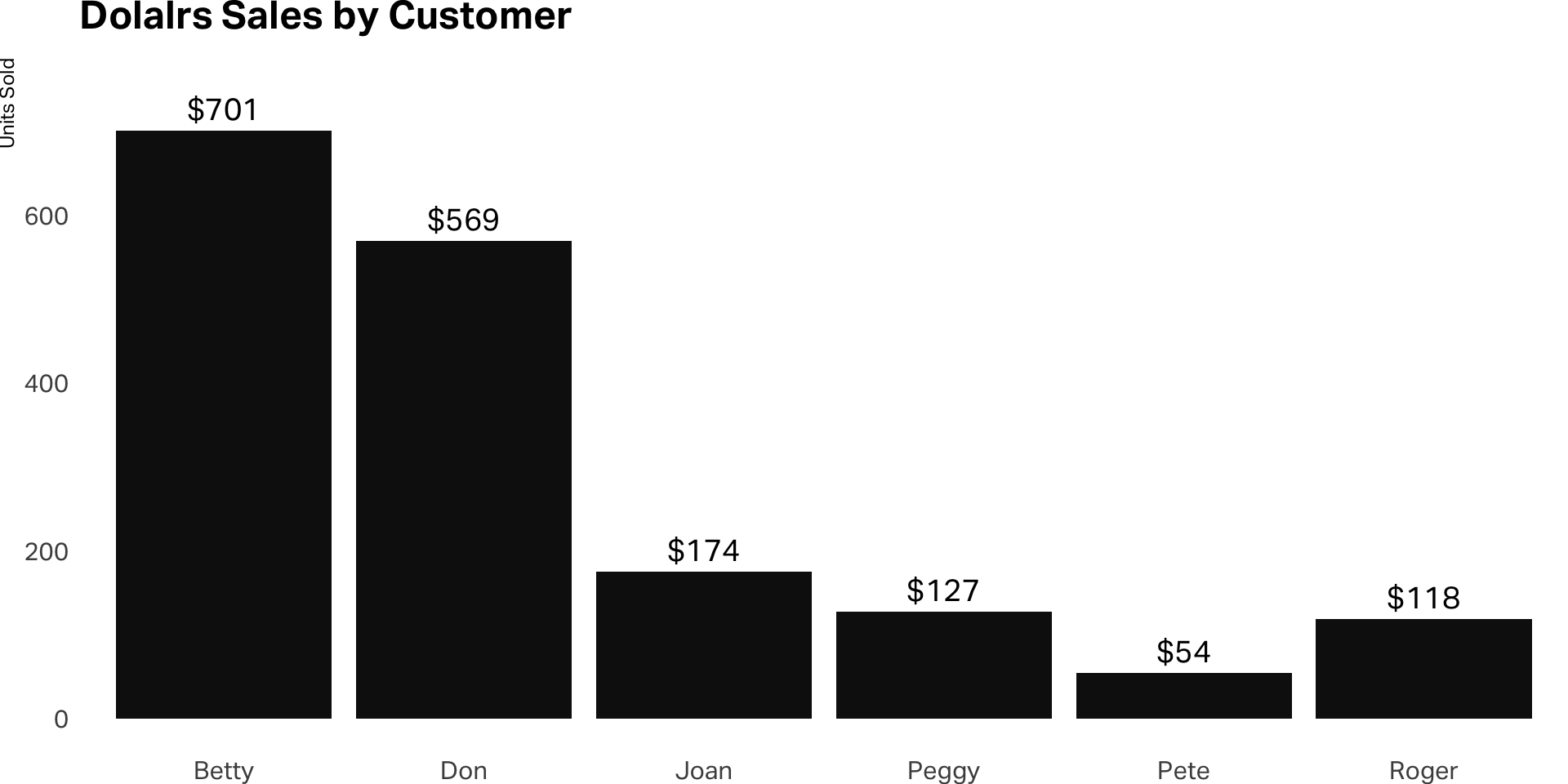
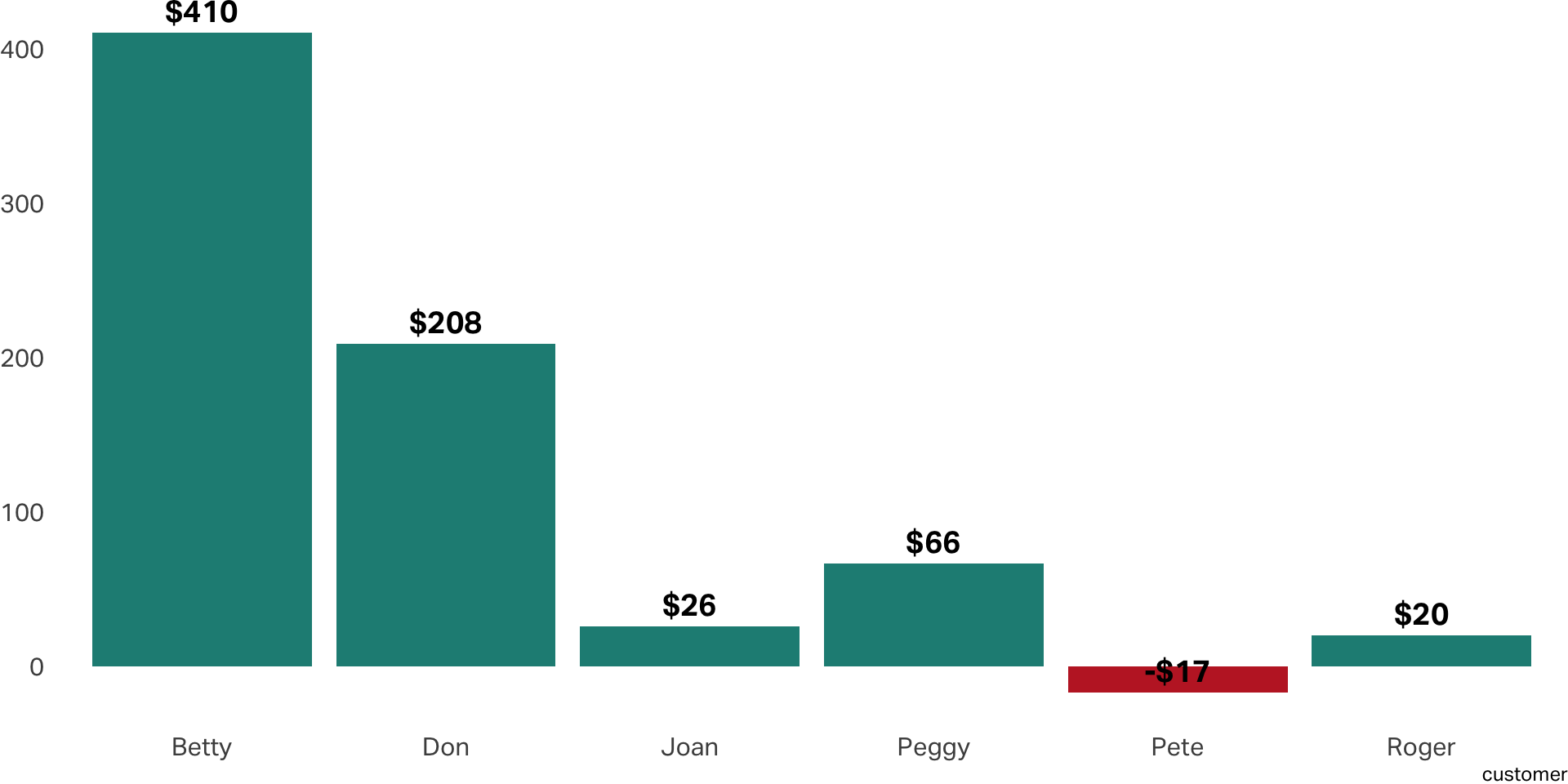
Revenue by customers
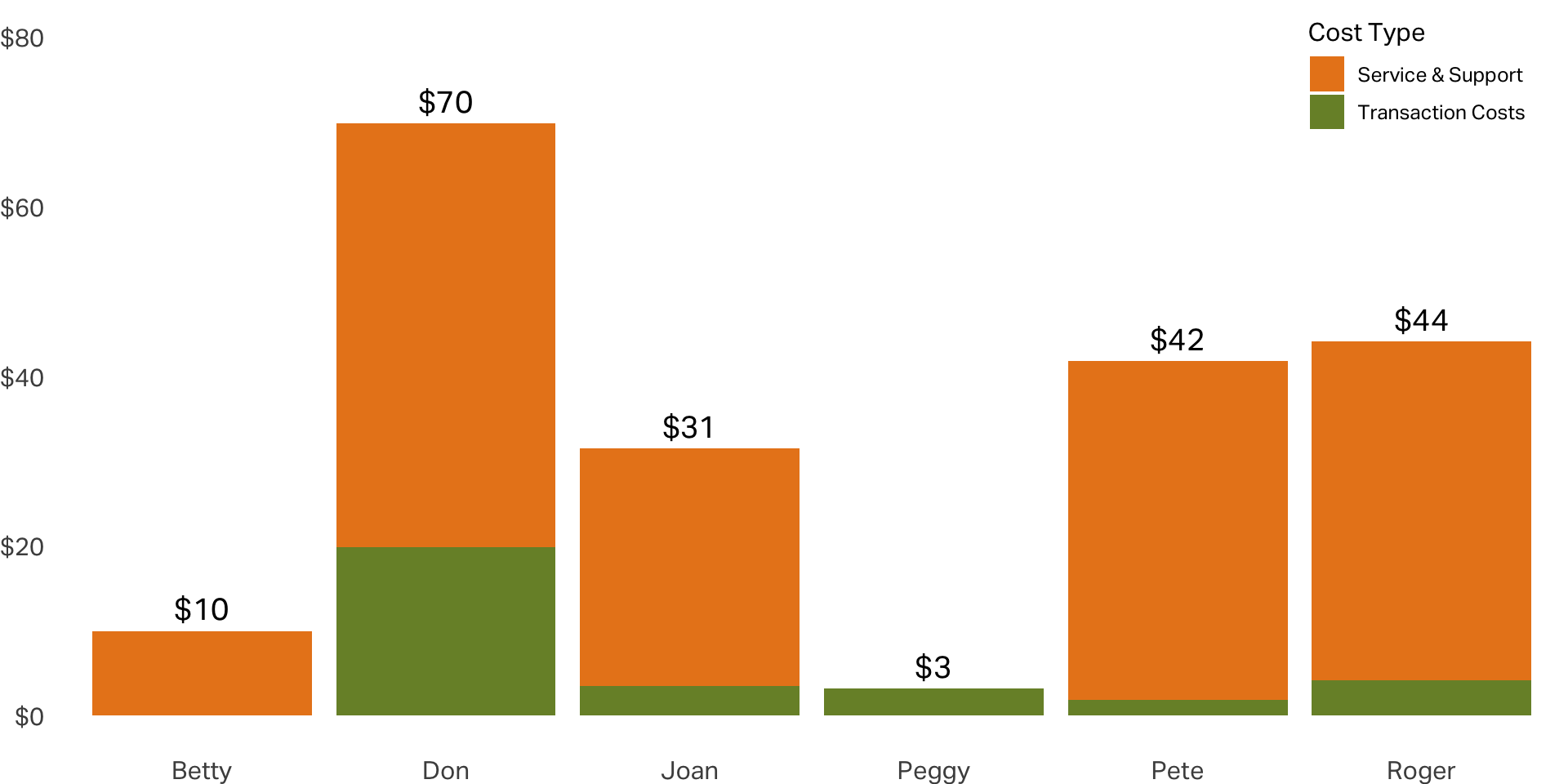
Customer-Related Costs
:::
Contribution
The profit generated by a customer or segment of customers after deducting the variable costs associated with serving them. It is calculated as the revenue generated by the customer minus the direct costs incurred in providing the goods or services to that customer.
Typical direct costs
- Cost of Goods Sold (COGS) Direct costs of producing or acquiring the product or service sold to the customer
- Marketing and Sales Expenses Costs related to acquiring, retaining, or developing the customer (e.g., advertising, promotions, referral commissions)
- Customer Service Costs Expenses incurred for supporting the customer, including call centers, online support, and complaint resolution
- Shipping and Handling Costs Any costs associated with delivering the product or service to the customer
- Return Costs Costs associated with product returns, including processing and restocking fees
- Transaction Fees Payment processing fees, such as credit card charges or transaction costs for online payments
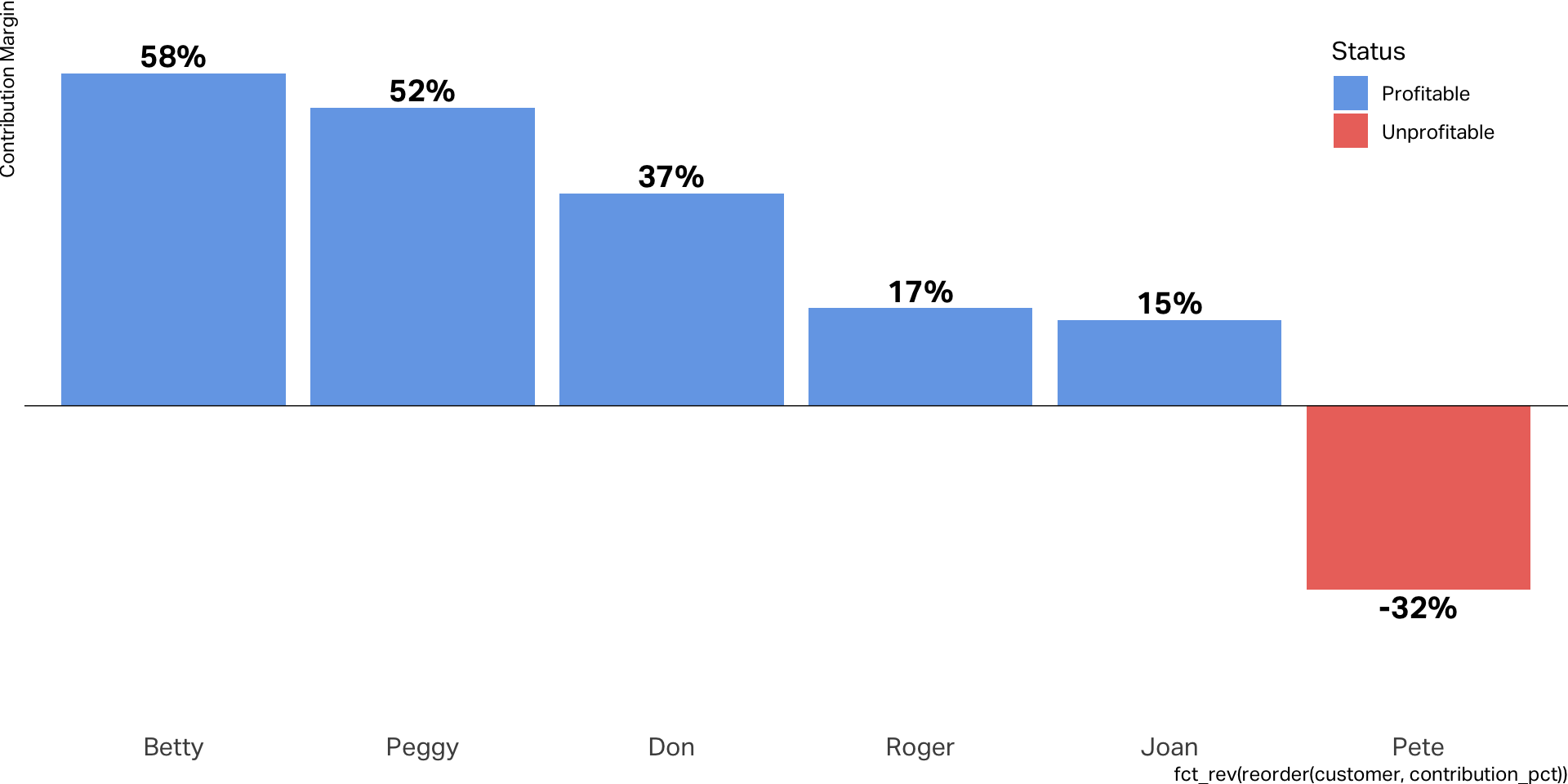
Customer Contribution
Contribution Margin
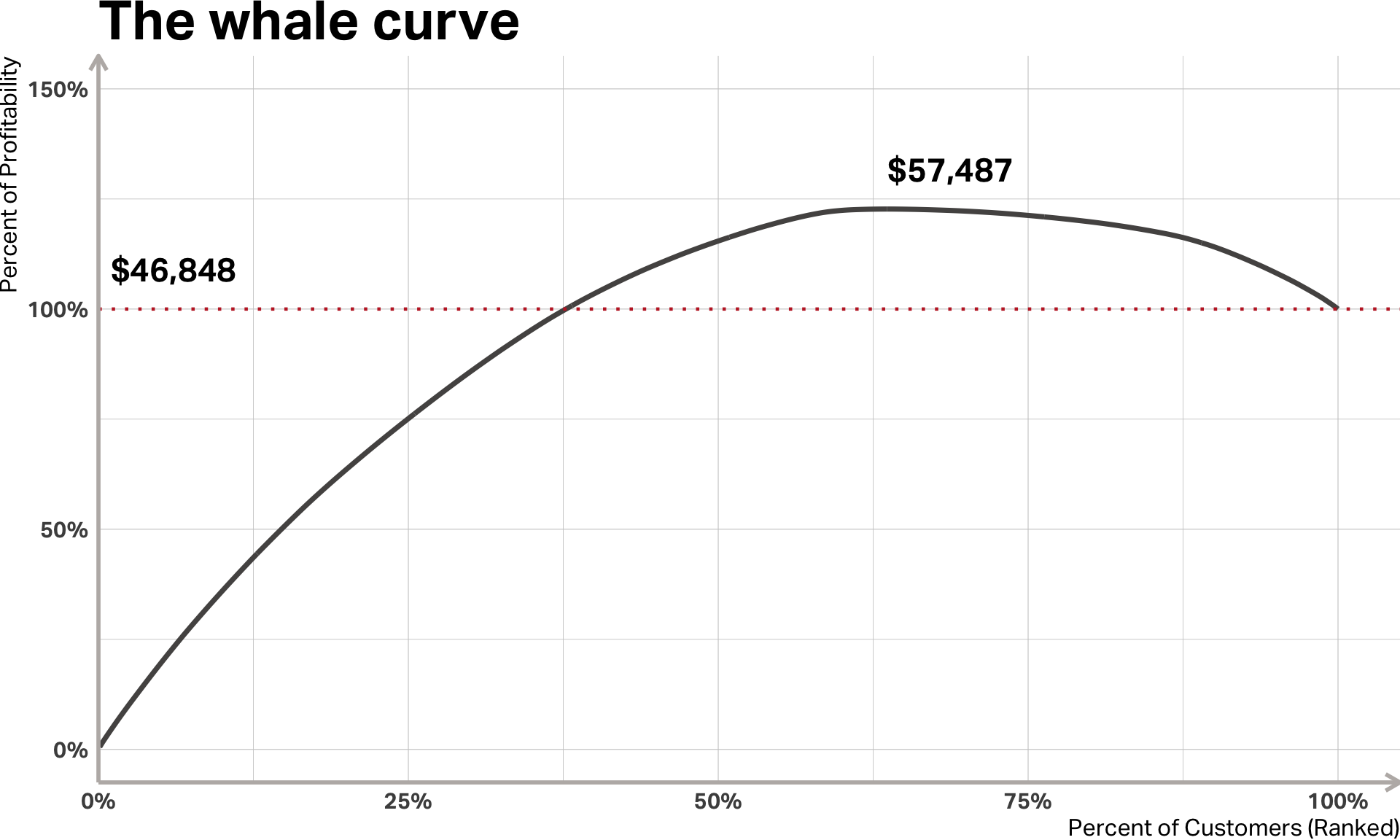
Forget average customers
Customer management

Customer
Lifetime Value
The present value of the expected net profit a business will generate from a customer over the entire duration of their relationship, calculated using discounted cash flow methods to account for the time value of money.
CLV’s parts
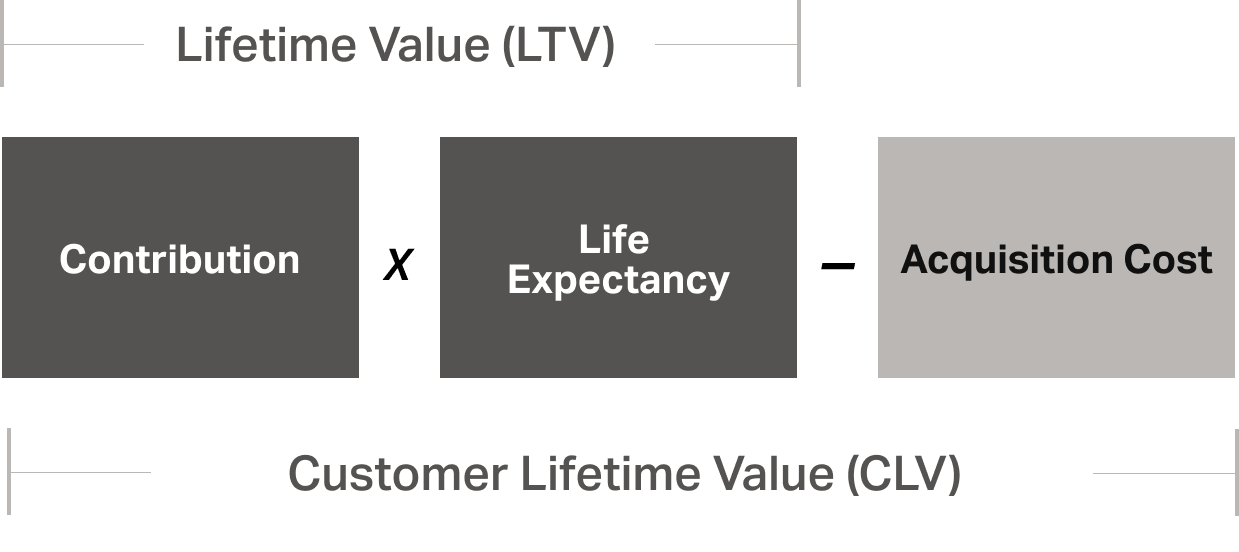
Required components
- Customer profit (Contribution)
- Retention rate
- Cost of capital (Discount factor)
- Customer acquisition cost (CAC)
Thinking in cohorts
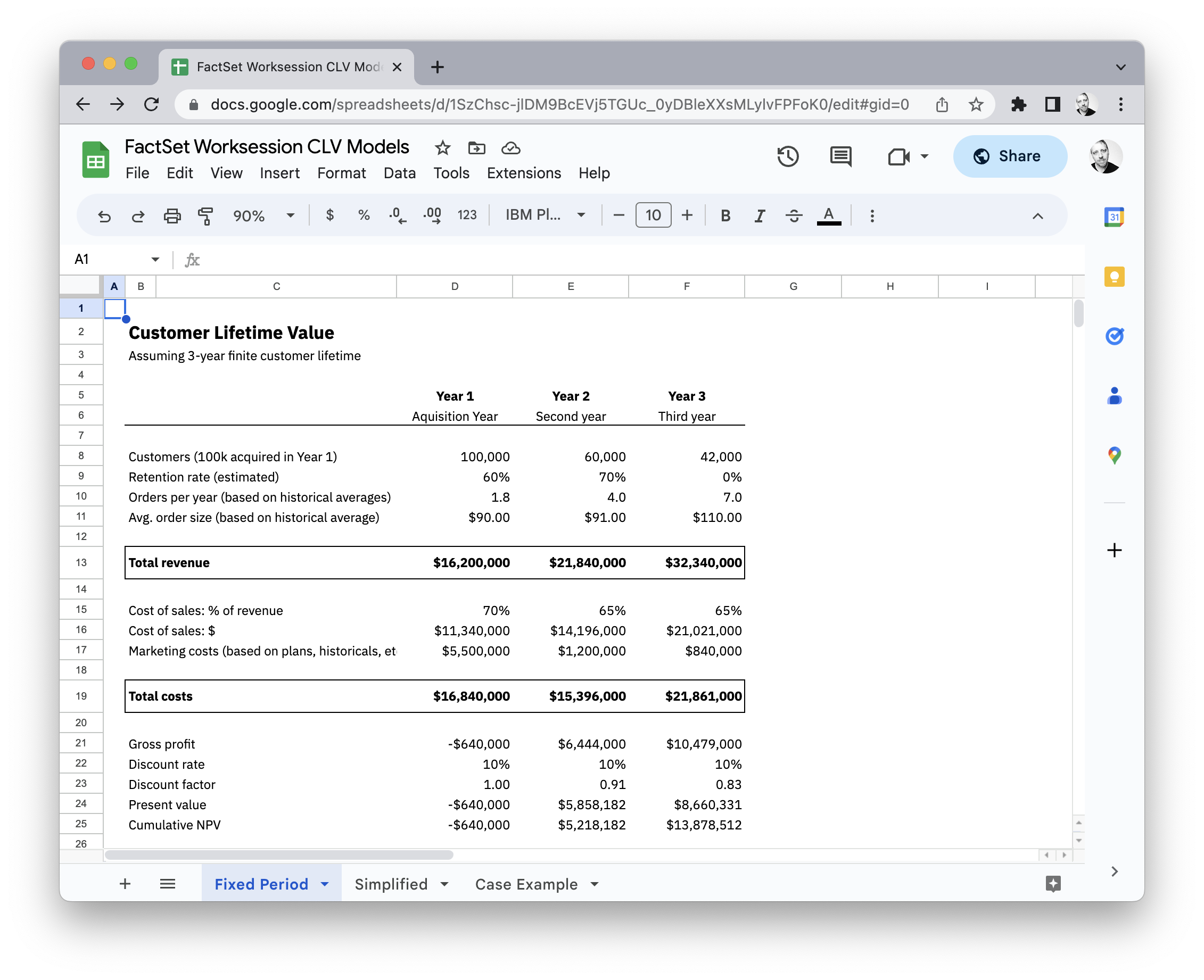
Year 1

Thinking in cohorts
Year 1

Year 2

Thinking in cohorts
Year 1

Year 2

Year 3

Retention and churn
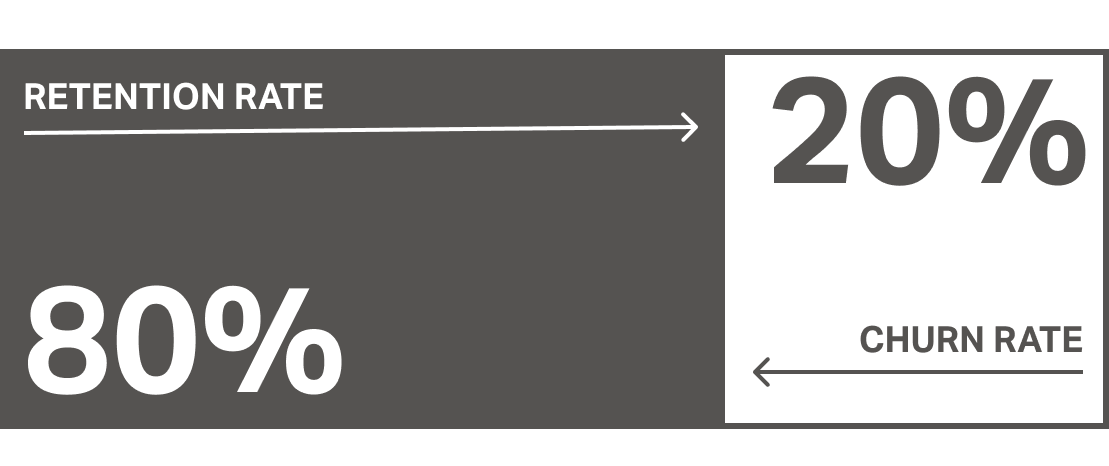
Retention mechanics
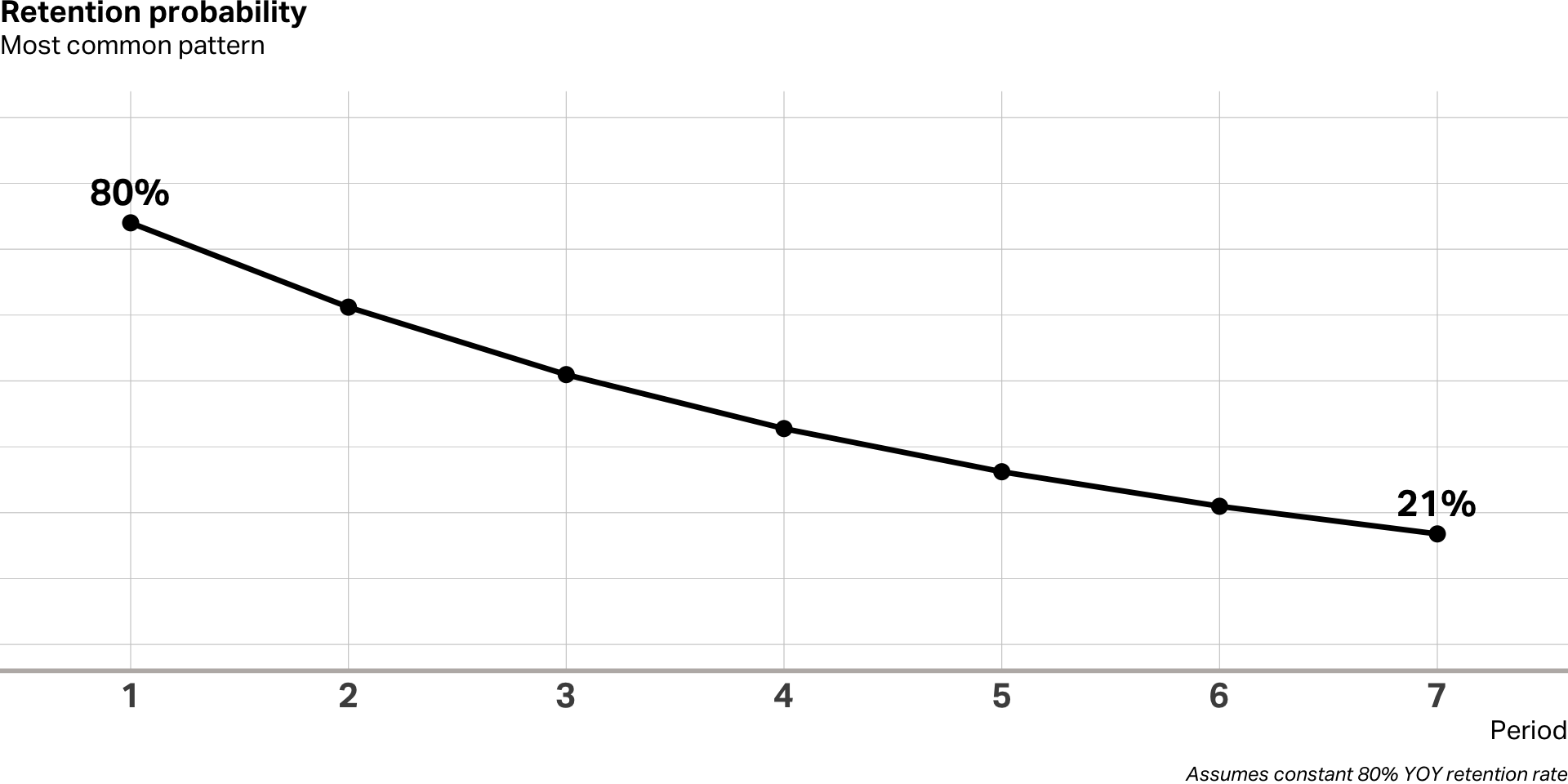
Calculating lifetime
How long should we expect to keep a customer in a cohort that averages an 80% monthly retention rate?
Calculating lifetime
How long should we expect to keep a customer in a cohort that averages an 80% monthly retention rate?
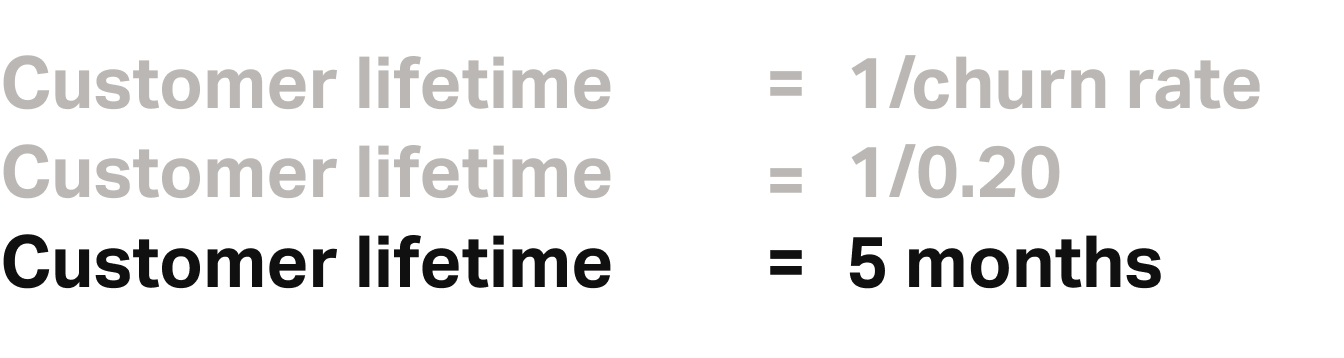
A customer generates $100 in monthly contribution.
The monthly churn rate is 20%.
What is the CLV of this customer?
Not so fast!
Money isn’t free.
How much is this customer worth?
A company has a customer that generates $100 contribution each month. The monthly churn rate is 20%. What is the CLV of this customer?
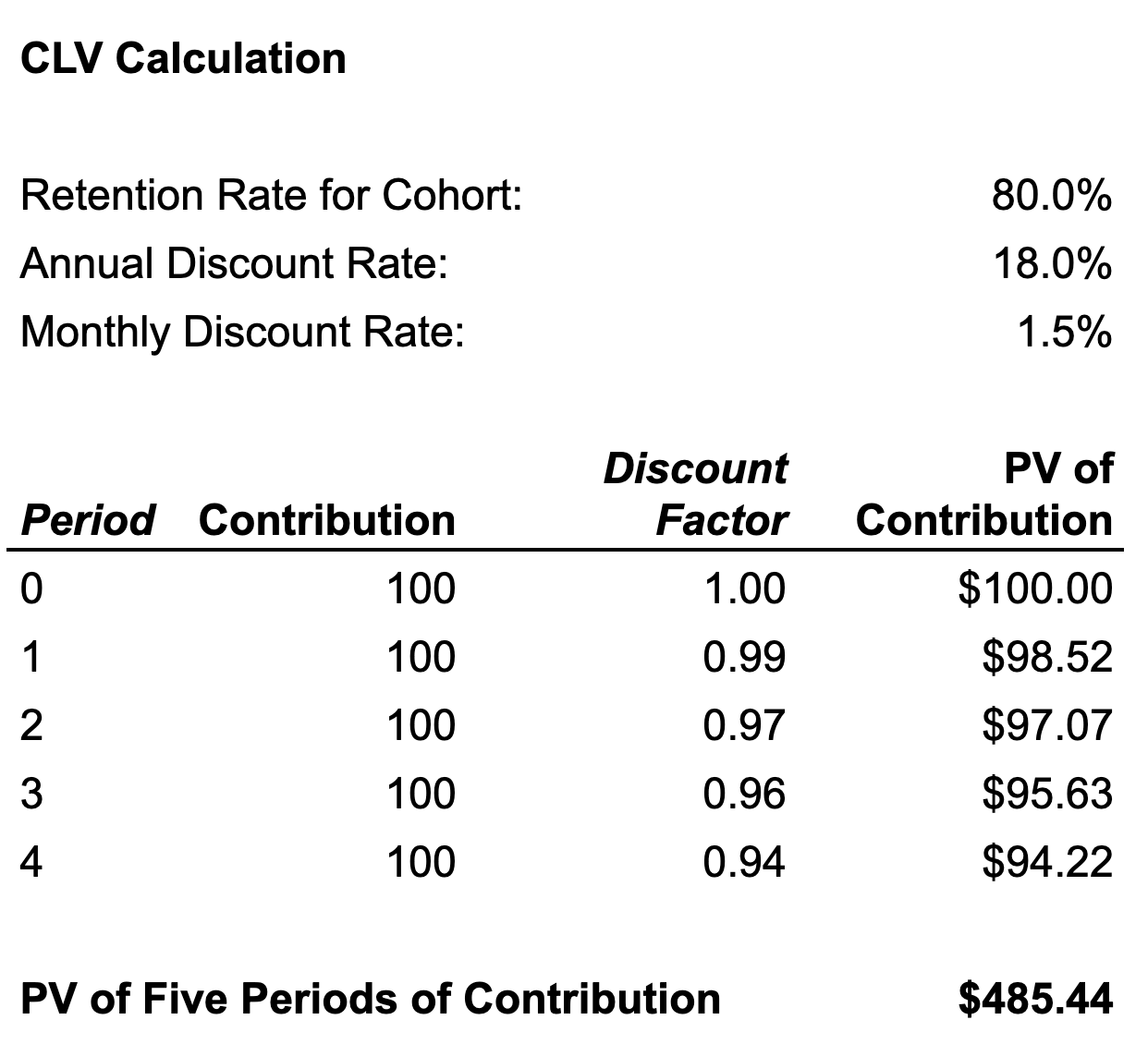
Hands-on
A simpler solution
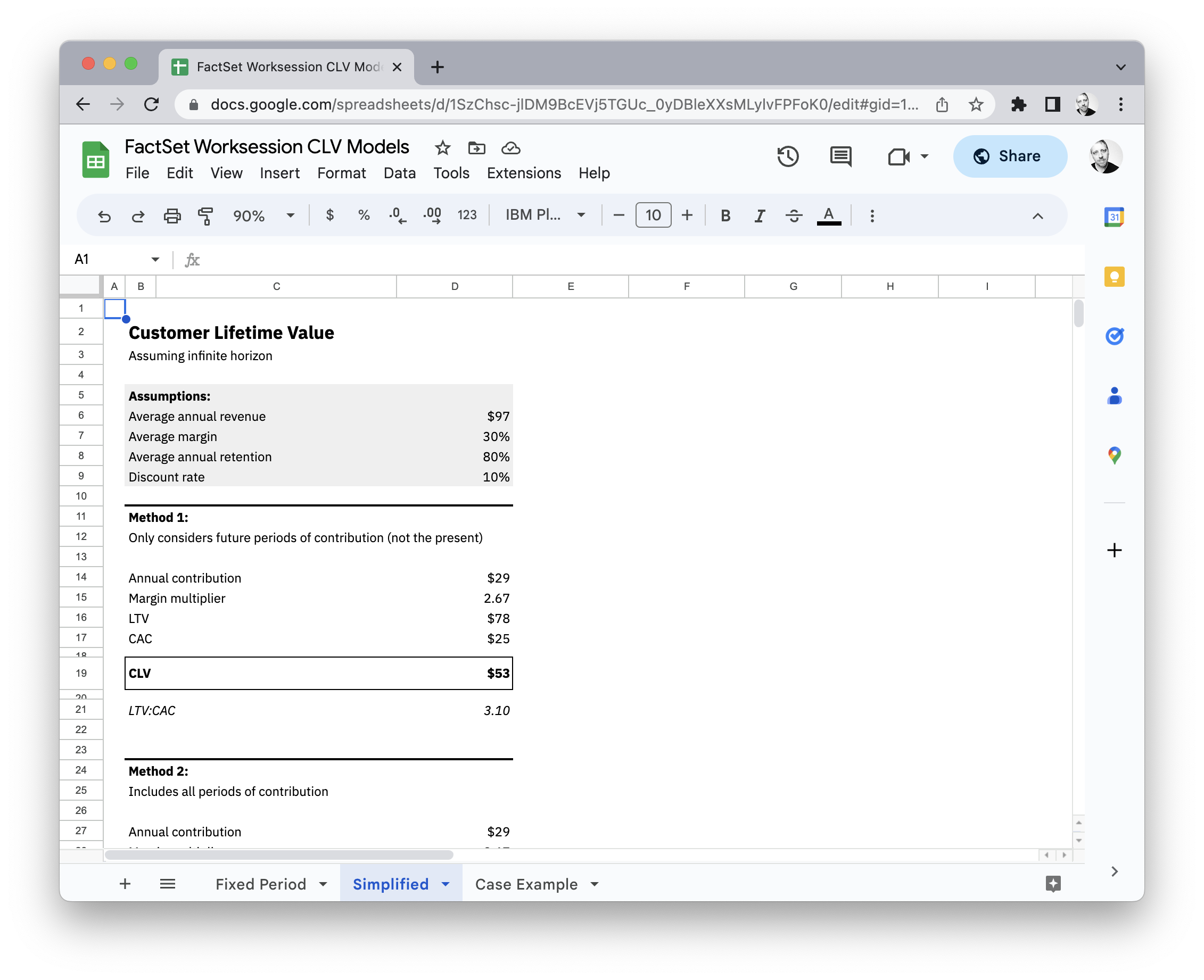
CLV simplified
Required assumptions
- Constant contribution average
- Constant retention rate
- Constant discount rate
- Value estimated over infinite time horizon
Simplification
Approaches
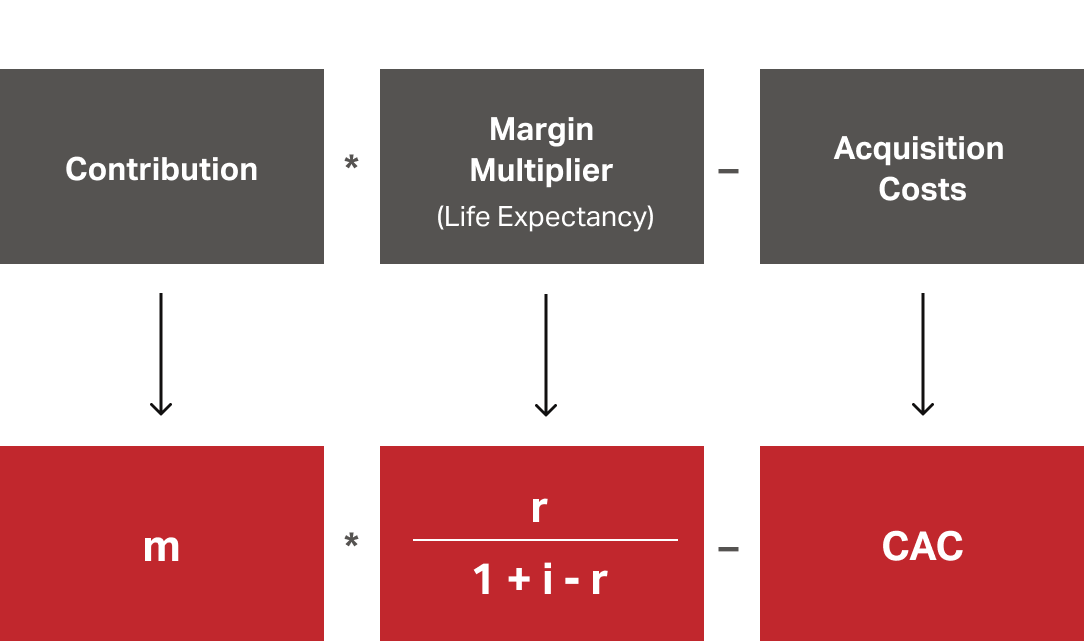
Base method
\[ \text{CLV} = m * \left(\frac{r}{1 + i - r}\right) \]
\[ m = \text{Contribution}\\ r = \text{Retention Rate}\\ i = \text{Discount Rate} \]
Alternate method
\[ \text{CLV} = m * \left(\frac{1 + i}{1 + i - r}\right) \]
\[ m = \text{Contribution}\\ r = \text{Retention Rate}\\ i = \text{Discount Rate} \]
Hands-on
When to use
Exclude present period
of contribution
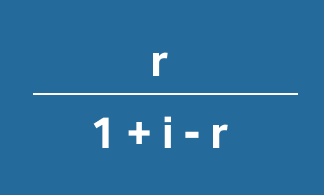
Include all periods
of contribution
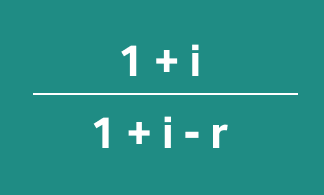
Acquisition costs
- Acquisition costs should only be deducted for new customers acquired in the forecast period
- Don’t deduct legacy acquisition costs for existing customers
- Ratios of LTV to CAC are used widely to manage costs and evaluate acquisition investments
Ratios

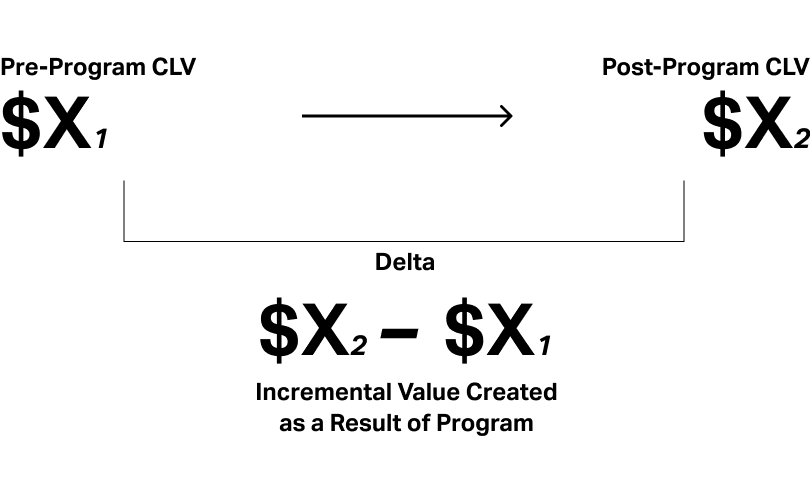
Delta analysis
Hands-on
Delta analysis

Key takeaways
Theory
- Estimates the total contribution of a customer throughout their lifetime of business with the firm
- Sensitive to fluctuations in period-over-period contribution and churn rates
- Expressed in present value of all future cash flows
Practice
- Simplified CLV model is good for quick decisions, but has limitations when there is significant variance in core components
- Delta analysis and LTV/CAC ratios are a good guide for investments
- Estimates have a shelf life; CLV is not static. It can be influenced by managerial decisions.